
 ≤
≤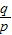 ≤
≤ ,试确定自然数k的最小值并说明理由.
,试确定自然数k的最小值并说明理由. 或大于
或大于 ,找到k的取值范围,然后根据抽屉原理证明k=10时,必有两个数属于同一个Ai,这两个数就是p、q,若p<q,则
,找到k的取值范围,然后根据抽屉原理证明k=10时,必有两个数属于同一个Ai,这两个数就是p、q,若p<q,则 ≤
≤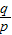 ≤
≤ 成立.
成立. ≤1≤
≤1≤ ,其他各组中任意两个自然数的比值均不小于
,其他各组中任意两个自然数的比值均不小于 且不大于
且不大于 .
. 或大于
或大于 ,这说明当k取9时,不一定能满足所要求的条件,∴k≥10.
,这说明当k取9时,不一定能满足所要求的条件,∴k≥10. ≤
≤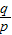 ≤
≤ 成立.
成立.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
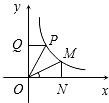 设P(a,b),M(c,d)是反比例函数y=
设P(a,b),M(c,d)是反比例函数y=| 1 |
| x |
| b |
| a |
| d |
| c |
查看答案和解析>>
科目:初中数学 来源: 题型:
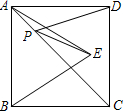 如图所示,正方形ABCD的面积为18,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图所示,正方形ABCD的面积为18,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )A、3
| ||
B、9
| ||
| C、6 | ||
| D、3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 20、如图,在△ABC中,点D,E分别是AB,AC边的中点,若把△ADE绕着点E顺时针旋转180°得到△CFE.
20、如图,在△ABC中,点D,E分别是AB,AC边的中点,若把△ADE绕着点E顺时针旋转180°得到△CFE.查看答案和解析>>
科目:初中数学 来源: 题型:
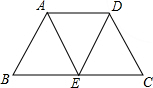 在等腰梯形ABCD中,AD∥BC,E是BC的中点,连接AE,DE,AE与DE相等吗?
在等腰梯形ABCD中,AD∥BC,E是BC的中点,连接AE,DE,AE与DE相等吗?查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com