
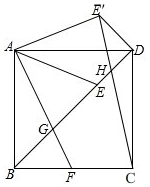
 如图,正方形ABCD中,F为BC边上的中点,连接AF交对角线BD于G,在BD上截BE=BA,连接AE,将△ADE沿AD翻折得△ADE′,连接E′C交BD于H,若BG=2,则四边形AGHE′的面积是$\frac{60}{7}$-$\frac{9}{14}\sqrt{2}$.
如图,正方形ABCD中,F为BC边上的中点,连接AF交对角线BD于G,在BD上截BE=BA,连接AE,将△ADE沿AD翻折得△ADE′,连接E′C交BD于H,若BG=2,则四边形AGHE′的面积是$\frac{60}{7}$-$\frac{9}{14}\sqrt{2}$. 分析 先连接EE',过G作BC的垂线,交BC于M,交AD于N,则MN⊥AD,运用勾股定理,等腰直角三角形的性质以及相似三角形的性质,求得△DE'H的面积,△ADG的面积以及△ADE'的面积,再根据四边形AGHE′的面积=△ADG的面积+△ADE'的面积-△DE'H的面积,进行计算即可.
解答  解:如图所示,连接EE',过G作BC的垂线,交BC于M,交AD于N,则MN⊥AD,
解:如图所示,连接EE',过G作BC的垂线,交BC于M,交AD于N,则MN⊥AD,
由BF∥AD可得,△BGF∽△DGA,
∴$\frac{BG}{DG}$=$\frac{BF}{DA}$
∵BG=2,F是BC的中点,
∴DG=4,BD=6,
∴等腰Rt△ABD中,AB=3$\sqrt{2}$,
∴BE=BA=3$\sqrt{2}$,
∴DE=6-3$\sqrt{2}$,
由折叠可得,AD⊥EE',∠EDE'=90°,
∴等腰Rt△DEE'中,EE'=$\sqrt{2}$DE=6$\sqrt{2}$-6,
△DEE'的面积=$\frac{1}{2}$DE2=$\frac{1}{2}$(6-3$\sqrt{2}$)2=27-18$\sqrt{2}$,
由EE'∥CD,可得△EE'H∽△DCE,
∴$\frac{EE'}{DC}$=$\frac{EH}{DH}$,即$\frac{EH}{DH}$=$\frac{6\sqrt{2}-6}{3\sqrt{2}}$=2-$\sqrt{2}$,
∴△DE'H的面积=△DEE'的面积×$\frac{1}{2-\sqrt{2}+1}$=(27-18$\sqrt{2}$)×$\frac{1}{3-\sqrt{2}}$=$\frac{45-27\sqrt{2}}{7}$,
∵Rt△BGM中,GM=$\sqrt{2}$,
∴GN=3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$,
∴△ADG的面积=$\frac{1}{2}$AD×GN=$\frac{1}{2}$×3$\sqrt{2}$×2$\sqrt{2}$=6,
又∵△ADE'的面积=$\frac{1}{2}$AD×$\frac{EE'}{2}$=$\frac{1}{2}$×3$\sqrt{2}$×(3$\sqrt{2}$-3)=9-$\frac{9}{2}\sqrt{2}$,
∴四边形AGHE′的面积=△ADG的面积+△ADE'的面积-△DE'H的面积=6+(9-$\frac{9}{2}\sqrt{2}$)-$\frac{45-27\sqrt{2}}{7}$=$\frac{60}{7}$-$\frac{9}{14}\sqrt{2}$.
故答案为:$\frac{60}{7}$-$\frac{9}{14}\sqrt{2}$.
点评 本题属于折叠问题,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.解决问题的关键是作辅助线构造相似三角形,依据相似三角形的对应边成比例,求得线段的长,进而得到三角形的面积.


科目:初中数学 来源: 题型:选择题
 如图,直线AC∥BD,AO、BO分别是∠BAC、∠ABD的平分线,那么下列结论错误的是( )
如图,直线AC∥BD,AO、BO分别是∠BAC、∠ABD的平分线,那么下列结论错误的是( )| A. | ∠BAO与∠CAO相等 | B. | ∠BAC与∠ABD互补 | C. | ∠BAO与∠ABO互余 | D. | ∠ABO与∠DBO不等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 弹簧总长L/cm | 16 | 17 | 18 | 19 | 20 |
| 重物质量x/千克 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
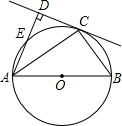 如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D
如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一组对边平行且另一组对边相等的四边形是平行四边形 | |
| B. | 两组对角都相等的四边形是平行四边形 | |
| C. | 一组对边平行且一组对角相等的四边形是平行四边形 | |
| D. | 一组对边平行,一组邻角互补的四边形是平行四边形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
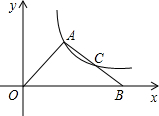 如图,△AOB中,点C为边AB的中点,反比例函数y=$\frac{k}{x}$(k>0)的图象经过A,C两点,若△AOB的面积为12,则k的值是( )
如图,△AOB中,点C为边AB的中点,反比例函数y=$\frac{k}{x}$(k>0)的图象经过A,C两点,若△AOB的面积为12,则k的值是( )| A. | 8 | B. | 7.5 | C. | 6 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知A.B两地相距100km,甲乙两人骑车同时分别从A,B两地相向而行.假设他们都保持匀速行驶.甲乙两人离A地的距离s(千米)与骑车时间t(小时)满足的函数关系图象如图所示.当甲乙两人相遇时,乙距离A地$\frac{300}{7}$km.
已知A.B两地相距100km,甲乙两人骑车同时分别从A,B两地相向而行.假设他们都保持匀速行驶.甲乙两人离A地的距离s(千米)与骑车时间t(小时)满足的函数关系图象如图所示.当甲乙两人相遇时,乙距离A地$\frac{300}{7}$km.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com