
【题目】已知:如图,在△ABC中,点D是BC的中点,过点D作直线交AB,CA的延长线于点E,F. 当BE=CF时,求证:AE=AF.

【答案】证明过程见解析
【解析】
试题分析:过点B作BG∥FC,延长FD交BG于点G,证明△BDG和△CDF全等,得到BG=CF,然后根据BE=CF,从而说明△BEG为等腰三角形,即∠G=∠BEG,根据平行可得∠G=∠F,根据对顶角可得∠BEG=∠AEF,根据等式的性质可得∠F=AEF,从而得出AE=AF.
试题解析:过点B作BG∥FC,延长FD交BG于点G.∴![]() .
.
∵点D是BC的中点,∴BD=CD.
在△BDG和△CDF中,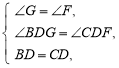
∴ △BDG≌△CDF. ∴BG=CF. ∵BE=CF, ∴BE=BG.
∴∠G=∠BEG ∵∠BEG=∠AEF ∴∠G=∠AEF ∴∠F=∠AEF ∴AE=AF


科目:初中数学 来源: 题型:
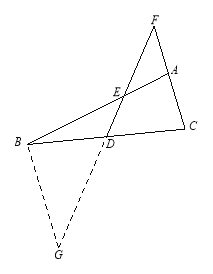
【题目】某班“数学兴趣小组”对函数![]() 的图像和性质进行了探究,探究过程如下,请补充完整.
的图像和性质进行了探究,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
| … |
|
|
|
| 0 | 1 | 2 | 3 | 4 | … |
| … | 3 |
|
|
| 0 |
| 0 |
| 3 | … |
其中,![]() =____________.
=____________.
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图像的一部分,请画出该图像的另一部分.
(3)观察函数图像,写出两条函数的性质:
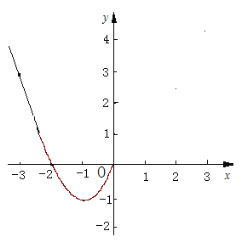
(4)进一步探究函数图像发现:
①函数图像与![]() 轴有__________个交点,所以对应方程
轴有__________个交点,所以对应方程![]() 有___________个实数根;
有___________个实数根;
②方程![]() 有___________个实数根;
有___________个实数根;
③关于![]() 的方程
的方程![]() 有4个实数根,
有4个实数根,![]() 的取值范围是_______________________
的取值范围是_______________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过正方形ABCD顶点B,C的⊙O与AD相切于点P,与AB,CD分别相交于点E、F,连接EF.
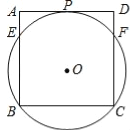
(1)求证:PF平分∠BFD.
(2)若tan∠FBC=![]() ,DF=
,DF=![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在网络上用“Google”搜索引擎搜索“中国梦”,能搜索到与之相关的结果个数约为45100000,这个数用科学记数法表示为( )
A. 451×105 B. 45.1×106 C. 4.51×107 D. 0.451×108
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com