
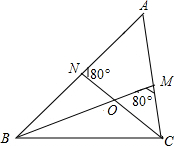
 如图,点O是△ABC两条内角平分线BM、CN的交点,若∠ANC=∠BMC=80°,则∠A=
如图,点O是△ABC两条内角平分线BM、CN的交点,若∠ANC=∠BMC=80°,则∠A=| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
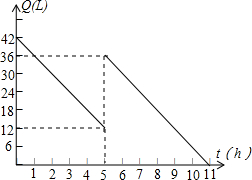 某机动车出发前油箱内有油42L,以40km/h匀速行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图回答问题.
某机动车出发前油箱内有油42L,以40km/h匀速行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图回答问题.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
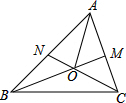 如图,点O是△ABC两条内角平分线BM、CN的交点,下列判断错误的是( )
如图,点O是△ABC两条内角平分线BM、CN的交点,下列判断错误的是( )| A、点O到△ABC三边距离相等 | ||
B、∠OBC+∠OCB=
| ||
| C、∠BOC-∠OAC=90° | ||
| D、∠BNC一定是钝角 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com