练习册

  • 练习册
  • 试题
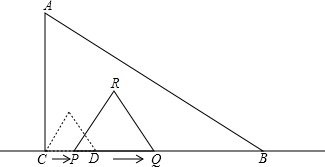
    精英家教网 > 初中数学 > 题目详情
    当x=-4时，的值等于
    [     ]
    A．4
    B．-4
    C．±4
    D．±2
    A
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    在Rt△ABC中，∠C=90°，BC=6cm，∠ABC=30°．D是CB上一点，DC=1cm．P、Q是直线CB上的两个动点，点P从C点出发，以1cm/s的速度沿直线CB向右运动，同时，点Q从D点出发，以2cm/s的速度沿直线CB向右运动，以PQ为一边在CB的上方作等边三角形PQR，如图是其运动过程中的某一位置．设运动的时间是t（s）．
    （1）△PQR的边长是
     
    cm（用含有t的代数式表示）；当t=
     
    时，点R落在AB上．
    （2）若等边△PQR与△ABC重叠部分的面积为y（cm2），求y与t之间的函数关系式，并写出自变量t的取值范围．
    （3）在P、Q移动的同时，以点A为圆心、tcm为半径的⊙A也在不断变化，请直接写出⊙A与△PQR的三边所在的直线相切时t的值．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图所示，菱形ABCD的边长为6厘米，∠B=60度．从初始时刻开始，点P、Q同时从A点出发，点P以1厘米/秒的速度沿A→C→B的方向运动，点Q以2厘米/秒的速度沿A→B→C→D的方向运动，当点Q运动到D点时，P、Q两点同时停止运动，设P、Q运动的时间为x秒时，△APQ与△ABC重叠部分精英家教网的面积为y平方厘米（这里规定：点和线段是面积为0的三角形），解答下列问题：
    （1）点P、Q从出发到相遇所用时间是
     
    秒；
    （2）点P、Q从开始运动到停止的过程中，当△APQ是等边三角形时x的值是
     
    秒；
    （3）求y与x之间的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图1，在Rt△AOB中，∠AOB=90°，AO=4
    		3
    ，∠ABO=30°．动点P在线段AB上从点A向终点B以每秒
    		3
    个单位的速度运动，设运动时间为t秒．在直线OB 上取两点M、N作等边△PMN．
    （1）求当等边△PMN的顶点M运动到与点O重合时t的值．
    （2）求等边△PMN的边长（用t的代数式表示）；
    （3）如果取OB的中点D，以OD为边在Rt△AOB 内部作如图2所示的矩形ODCE，点C在线段AB上．设等边△PMN和矩形ODCE重叠部分的面积为S，请求出当0≤t≤2秒时S与t的函数关系式，并求出S的最大值．
    （4）在（3）中，设PN与EC的交点为R，是否存在点R，使△ODR是等腰三角形？若存在，求出对应的t的值；若不存在，请说明理由．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，抛物线y=ax2+bx+2
    		3
    交x轴于点B（6，0）和C（-2，0），交y轴于点A．动点P在线段AB上从点A向点B以每秒
    		3
    2
    个单位的速度运动，设运动时间为t秒．在x轴上取两点M，N作等边△PMN．
    （1）求抛物线和直线AB的解析式；
    （2）求等边△PMN的边长（用t的代数式表示），并求出当等边△PMN的顶点P运动到抛物线对称轴上时t的值；
    （3）如果取AB的中点D，过D作DE⊥y轴，DF⊥x轴，垂足分别为E、F．设等边△PMN和矩形OEDF重叠部分的面积为S，请求出当0≤t≤2秒时S与t的函数关系式，并求出S的最大值．

    查看答案和解析>>

    科目：初中数学 来源：2015届湖北十堰市茅箭区实验学校八年级上期中考试数学试卷（解析版） 题型：解答题

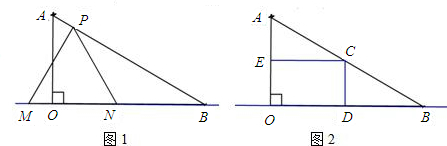
    如图1，点A在x轴上，点D在y轴上，以OA、AD为边分别作等边△OAC和等边△ADE，若D（0，4），A（2，0）.

    （1）若∠DAC=10°，求CE的长和∠AEC的度数.

    （2）如图2，若点P为x轴正半轴上一动点，点P在点A的右边，连PC，以PC为边在第一象限作等边△PCM，延长MA交y轴于N，当点P运动时.

    ①∠ANO的值是否发生变化？若不变，求其值，若变化，请说明理由.

    ②AM-AP的值是否发生变化？若不变，求其值，若变化，请说明理由.

     

    查看答案和解析>>

    同步练习册答案