
【题目】九年级某班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
时间x(天) | 1 | 30 | 60 | 90 |
每天销售量p(件) | 198 | 140 | 80 | 20 |
(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.
【答案】(1)w=![]() ;(2)销售第45天时,当天获得的销售利润最大,最大利润是6050元;(3)该商品在销售过程中,共有24天每天的销售利润不低于5600元.
;(2)销售第45天时,当天获得的销售利润最大,最大利润是6050元;(3)该商品在销售过程中,共有24天每天的销售利润不低于5600元.
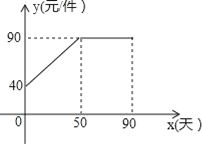
【解析】试题分析:(1)当1≤x≤50时,设商品的售价y与时间x的函数关系式为y=kx+b,由点的坐标利用待定系数法即可求出此时y关于x的函数关系式,根据图形可得出当50≤x≤90时,y=90.再结合给定表格,设每天的销售量p与时间x的函数关系式为p=mx+n,套入数据利用待定系数法即可求出p关于x的函数关系式,根据销售利润=单件利润×销售数量即可得出w关于x的函数关系式;
(2)根据w关于x的函数关系式,分段考虑其最值问题.当1≤x≤50时,结合二次函数的性质即可求出在此范围内w的最大值;当50≤x≤90时,根据一次函数的性质即可求出在此范围内w的最大值,两个最大值作比较即可得出结论;
(3)令w≥5600,可得出关于x的一元二次不等式和一元一次不等式,解不等式即可得出x的取值范围,由此即可得出结论.
试题解析:(1)当1≤x≤50时,设商品的售价y与时间x的函数关系式为y=kx+b(k、b为常数且k≠0),
∵y=kx+b经过点(0,40)、(50,90),
∴![]() ,解得
,解得![]() ,
,
∴售价y与时间x的函数关系式为y=x+40;
当50≤x≤90时,y=90.
∴售价y与时间x的函数关系式为y=![]() .
.
由数据可知每天的销售量p与时间x成一次函数关系,
设每天的销售量p与时间x的函数关系式为p=mx+n(m、n为常数,且m≠0),
∵p=mx+n过点(60,80)、(30,140),
∴![]() ,解得:
,解得: ![]() ,
,
∴p=﹣2x+200(0≤x≤90,且x为整数),
当1≤x≤50时,w=(y﹣30)p=(x +40﹣30)(﹣2 x +200)=﹣2 x 2+180 x +2000;
当50≤x≤90时,w=(90﹣30)(﹣2 x +200)=﹣120 x +12000.
综上所示,每天的销售利润w与时间x的函数关系式是w=![]() .
.
(2)当1≤x≤50时,w=﹣2 x 2+180 x +2000=﹣2(x﹣45)2+6050,
∵a=﹣2<0且1≤x≤50,
∴当x =45时,w取最大值,最大值为6050元.
当50≤x≤90时,w=﹣120 x +12000,
∵k=﹣120<0,w随x增大而减小,
∴当x =50时,w取最大值,最大值为6000元.
∵6050>6000,
∴当x =45时,w最大,最大值为6050元.
即销售第45天时,当天获得的销售利润最大,最大利润是6050元.
(3)当1≤x≤50时,令w=﹣2x2+180x+2000≥5600,即﹣2x2+180x﹣3600≥0,
解得:30≤x≤50,
50﹣30+1=21(天);
当50≤x≤90时,令w=﹣120 x +12000≥5600,即﹣120 x +6400≥0,
解得:50≤x≤53![]() ,
,
∵x为整数,
∴50≤x≤53,
53﹣50+1=4(天).
综上可知:21+4﹣1=24(天),
故该商品在销售过程中,共有24天每天的销售利润不低于5600元.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】下列整式乘法运算中,正确的是( )
A.(x-y)(y+ x)=x2-y2 B.(a+3)2=a2+9
C.(a+b)(-a-b)=a2-b2 D.(x-y)2=x2-y2
查看答案和解析>>
科目:初中数学 来源: 题型:
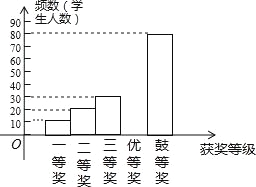
【题目】国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》,这是中国足球历史上的重大改革.为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次 | 频数 | 频率 |
一等奖 | 10 | 0.05 |
二等奖 | 20 | 0.10 |
三等奖 | 30 | b |
优胜奖 | a | 0.30 |
鼓励奖 | 80 | 0.40 |
请根据所给信息,解答下列问题:
(1)a= ,b= ,且补全频数分布直方图;
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表我市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com