
 的顶点坐标为(0,2),矩形ABCD的顶点B.C在x轴上,A.D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内。
的顶点坐标为(0,2),矩形ABCD的顶点B.C在x轴上,A.D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内。
 x2+2;(2)p=-(x+2)2+8,其中-2<x<2;(3)不存在,证明见解析.
x2+2;(2)p=-(x+2)2+8,其中-2<x<2;(3)不存在,证明见解析. ,即可求得抛物线的解析式;
,即可求得抛物线的解析式; ,
, x2+2;
x2+2; x2+2)-4x=-(x+2)2+8.
x2+2)-4x=-(x+2)2+8.

科目:初中数学 来源:不详 题型:解答题
 轴于点
轴于点 ,交
,交 轴于
轴于 ,
, 两点(点
两点(点 在点
在点 的左侧),已知
的左侧),已知 点坐标为(6,0).
点坐标为(6,0).
 作线段
作线段 的垂线交抛物线于点
的垂线交抛物线于点 ,如果以点
,如果以点 为圆心的圆与抛物线的对称轴
为圆心的圆与抛物线的对称轴 相切,先补全图形,再判断直线
相切,先补全图形,再判断直线 与⊙
与⊙ 的位置关系并加以证明;
的位置关系并加以证明; 是抛物线上的一个动点,且位于
是抛物线上的一个动点,且位于 ,
, 两点之间.问:当点
两点之间.问:当点 运动到什么位置时,
运动到什么位置时, 的面积最大?求出
的面积最大?求出 的最大面积.
的最大面积.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 .
. 的图象与
的图象与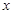 轴两个交点的横坐标均为整数,且k为正整数,求k值并用配方法求出抛物线的顶点坐标;
轴两个交点的横坐标均为整数,且k为正整数,求k值并用配方法求出抛物线的顶点坐标;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
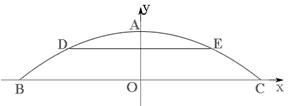
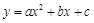 图象中,观察得出了下面的五条信息:①
图象中,观察得出了下面的五条信息:①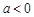 ,②
,②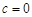 ,③函数的最小值为
,③函数的最小值为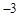 ,④当
,④当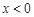 时,
时,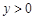 ,⑤当
,⑤当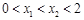 时,
时,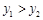 (6)对称轴是直线x=2.你认为其中正确的个数为( )
(6)对称轴是直线x=2.你认为其中正确的个数为( )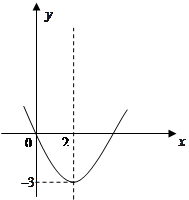
| A.2 | B.3 | C.4 | D.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com