
 .
. 的图象与
的图象与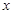 轴两个交点的横坐标均为整数,且k为正整数,求k值并用配方法求出抛物线的顶点坐标;
轴两个交点的横坐标均为整数,且k为正整数,求k值并用配方法求出抛物线的顶点坐标; 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源:不详 题型:解答题
 天销售的相关信息如下表所示.
天销售的相关信息如下表所示.| 销售量p(张) |  |
| 销售单价q(元/张) |  |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的顶点坐标为(0,2),矩形ABCD的顶点B.C在x轴上,A.D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内。
的顶点坐标为(0,2),矩形ABCD的顶点B.C在x轴上,A.D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内。
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 经过点A和点C,动点P在x轴上以每秒1个长度单位的速度由抛物线与x轴的另一个交点B向点A运动,点Q由点C沿线段CA向点A运动且速度是点P运动速度的2倍.
经过点A和点C,动点P在x轴上以每秒1个长度单位的速度由抛物线与x轴的另一个交点B向点A运动,点Q由点C沿线段CA向点A运动且速度是点P运动速度的2倍.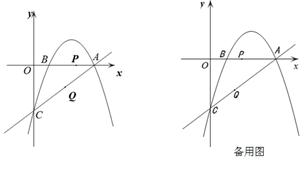
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com