

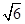 或4+
或4+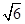 ; ②存在一点P,使△PAD是以AD为斜边的直角三角形, P(﹣2,1)或(﹣2,2).
; ②存在一点P,使△PAD是以AD为斜边的直角三角形, P(﹣2,1)或(﹣2,2).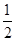 (AB+CD)•OD=9,
(AB+CD)•OD=9,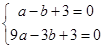 ,
, .
.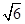 或4+
或4+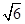 秒时,△PAD是以AD为腰的等腰三角形.
秒时,△PAD是以AD为腰的等腰三角形.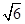 或4+
或4+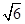 .
.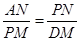 ,
,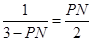 ,
,

科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
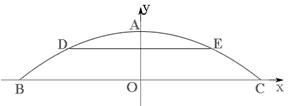
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 .
. 的图象与
的图象与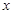 轴两个交点的横坐标均为整数,且k为正整数,求k值并用配方法求出抛物线的顶点坐标;
轴两个交点的横坐标均为整数,且k为正整数,求k值并用配方法求出抛物线的顶点坐标;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| x | … | | | | | | … |
| y | … | | | | | | … |
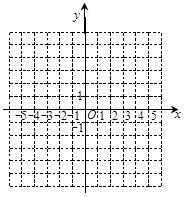
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
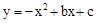 上部分点的横坐标
上部分点的横坐标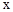 ,纵坐标
,纵坐标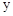 的对应值如下表:
的对应值如下表: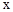 | … |  |  | 0 | 1 | 2 | … |
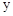 | … | 0 | 4 | 6 | 6 | 4 | … |
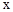 轴的一个交点为
轴的一个交点为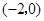 ; ②抛物线与
; ②抛物线与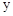 轴的交点为
轴的交点为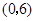 ;
;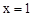 ; ④在对称轴左侧
; ④在对称轴左侧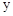 随
随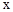 增大而增大.
增大而增大.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
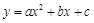 图象中,观察得出了下面的五条信息:①
图象中,观察得出了下面的五条信息:①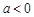 ,②
,②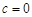 ,③函数的最小值为
,③函数的最小值为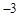 ,④当
,④当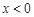 时,
时,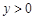 ,⑤当
,⑤当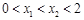 时,
时,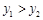 (6)对称轴是直线x=2.你认为其中正确的个数为( )
(6)对称轴是直线x=2.你认为其中正确的个数为( )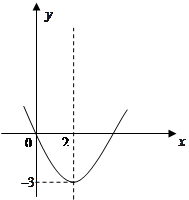
| A.2 | B.3 | C.4 | D.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com