
 经过点A和点C,动点P在x轴上以每秒1个长度单位的速度由抛物线与x轴的另一个交点B向点A运动,点Q由点C沿线段CA向点A运动且速度是点P运动速度的2倍.
经过点A和点C,动点P在x轴上以每秒1个长度单位的速度由抛物线与x轴的另一个交点B向点A运动,点Q由点C沿线段CA向点A运动且速度是点P运动速度的2倍.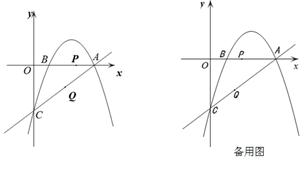
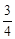 x-3,抛物线解析式为
x-3,抛物线解析式为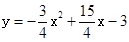 ;
;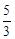 ,②t=
,②t=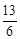 ;(3)存在,理由见解析.
;(3)存在,理由见解析.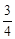 .
.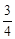 x-3.
x-3.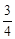 x-3与y轴交于点C,可知C(0,-3).
x-3与y轴交于点C,可知C(0,-3).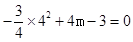 ,解得m=
,解得m=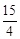 .
.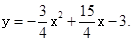
 ,
,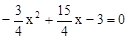 ,解得x1=1,x2=4.
,解得x1=1,x2=4.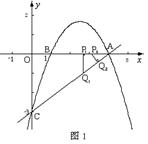
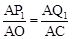 ,∴
,∴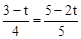 .解得t=
.解得t=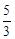 ;
;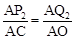 ,∴
,∴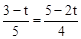 .解得t=
.解得t=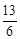 ;
;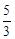 或
或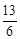 时,以P、Q、A为顶点的三角形与△AOC相似.
时,以P、Q、A为顶点的三角形与△AOC相似.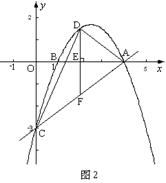
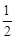 ×4(DE+EF)=2×(
×4(DE+EF)=2×(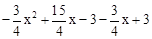 )=
)=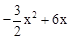 .
.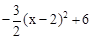 (0<x<4).
(0<x<4).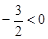 ,∴当x=2时,S△ACD的面积最大.
,∴当x=2时,S△ACD的面积最大.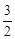 .
.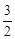 ).
).

科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 .
. 的图象与
的图象与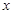 轴两个交点的横坐标均为整数,且k为正整数,求k值并用配方法求出抛物线的顶点坐标;
轴两个交点的横坐标均为整数,且k为正整数,求k值并用配方法求出抛物线的顶点坐标;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| x | … | | | | | | … |
| y | … | | | | | | … |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
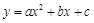 图象中,观察得出了下面的五条信息:①
图象中,观察得出了下面的五条信息:①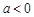 ,②
,②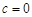 ,③函数的最小值为
,③函数的最小值为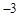 ,④当
,④当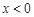 时,
时,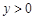 ,⑤当
,⑤当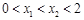 时,
时,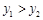 (6)对称轴是直线x=2.你认为其中正确的个数为( )
(6)对称轴是直线x=2.你认为其中正确的个数为( )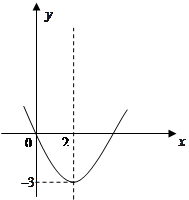
| A.2 | B.3 | C.4 | D.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com