
 如图,GC交AB于点M,GH分别交AB,EF于点N,HD平分∠GHF,∠1+∠C=180°,∠2=∠3=60°,求证:CD∥EF.
如图,GC交AB于点M,GH分别交AB,EF于点N,HD平分∠GHF,∠1+∠C=180°,∠2=∠3=60°,求证:CD∥EF. 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、对应边成比例的多边形 |
| B、四个角都对应相等的两个梯形 |
| C、有一个角相等的两个菱形 |
| D、各边对应成比例的两个平行四边形 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 甲乙两船同时从港口O出发,甲船以16.1海里/小时的速度向东偏南35°方向航行,乙船向西偏南58°方向航行,航行了两小时,甲船到达A处并观测到B处的乙船恰好在其正西方向.求乙船的速度v(精确到0.1海里/小时).
甲乙两船同时从港口O出发,甲船以16.1海里/小时的速度向东偏南35°方向航行,乙船向西偏南58°方向航行,航行了两小时,甲船到达A处并观测到B处的乙船恰好在其正西方向.求乙船的速度v(精确到0.1海里/小时).查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,斜坡AC的坡度(坡高比水平距离)为1:
如图,斜坡AC的坡度(坡高比水平距离)为1:| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
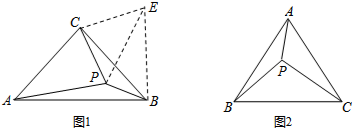
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com