

分析 ①通过旋转作辅助三角形ADC,由旋转的性质得:BE=DC,AE=AD,∠EAD=∠BAC=60,可得等边三角形AED,由此可得△CDE即所构三角形;
②先根据周角的定义求∠AEB的度数,再由全等得:∠ADC=∠AEB=124°,利用等边三角形每个角都是60°分别计算所构成的三角形各角的度数即可.
解答 证明:①∵△ABC是等边三角形,
∴AB=BC=CA;∠ACB=60°,
∴将△BEC绕点C逆时针旋转60°,至△ACD,BC与AC重合,连接ED,
∴△ADC≌△AEB,
∴AD=AE,BE=CD,∠EAD=60°,
∴△AED是等边三角形,
∴ED=AE,
∴以AE、BE、CE为边可以构成一个三角形,△CDE即所构三角形;
②∵∠BEC=113°,∠AEC=123°,
∴∠AEB=360°-113°-123°=360°-236°=124°,
由△ADC≌△AEB得:∠ADC=AEB=124°,
∴∠EDC=124°-60°=64°,
∠DEC=123°-60°=63°,
∴∠ECD=180°-64°-63°=53°,
∴构成三角形的各角度数分别为:63°、53°、64°.
点评 本题考查了等边三角形的性质和判定、旋转的性质、全等三角形的性质,明确旋转前后的两个三角形是全等形,并熟练掌握等边三角形的性质和判定.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
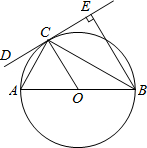 如图,AB是⊙O的直径,CD是⊙O的切线,切点为C,BE⊥CD,垂足为E,连接AC、BC.
如图,AB是⊙O的直径,CD是⊙O的切线,切点为C,BE⊥CD,垂足为E,连接AC、BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com