
如图13,矩形ABCD的对角线AC、BD相交于点O,E、F分别是OA、OB的中点.
(1)试问:△ADE与△BCF全等吗?请说明理由
(2)若AD = 4cm,AB = 8cm,求CF的长.
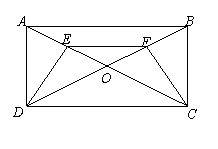
(1)证明:∵四边形ABCD为矩形,∴AD=BC,OA=OC,OB=OD,AC=BD, AD∥BC,
∴OA=OB=OC,∠DAE=∠OCB,∴∠OCB=∠OBC,∴∠DAE=∠CBF.
又∵AE=![]() OA,BF=
OA,BF=![]() OB,∴AE=BF,∴△ADE≌△BCF.
OB,∴AE=BF,∴△ADE≌△BCF.
(2)解:过点F作FG⊥CD于点G,则∠DGF=90º,
∵∠DCB=90º,∴∠DGF=∠DCB,又∵∠FDG=∠BDC
∴△DFG∽△DBC,
![]() ∴
∴![]() .
.
由(1)可知DF=3FB,得![]() ,∴
,∴![]() ,∴FG=3,DG=6,
,∴FG=3,DG=6,
∴GC=DC-DG=8-6=2.
在Rt△FGC中,![]() cm.
cm.
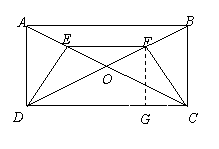
(说明:还有其他解法,如延长CF交AB于点H,利用△DFC∽△BFH计算.)


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
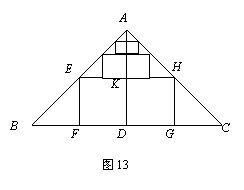
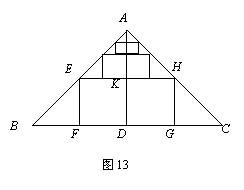
已知:如图13,等腰△ABC中,底边BC=12,高AD=6.
(1)在△ABC内作矩形EFGH,使F、G在BC上,E、H分别在AB、AC上,且长是宽的2倍.求矩形EFGH的面积.
(2)在(1)的基础上,再作第二个矩形,使其两个顶点在EH上,另外两个顶点分别在AB、AC上,且长是宽的2倍.则第二个矩形的面积为 ;
(3)在(2)的基础上,再作第三个矩形,使其两个顶点在第二个矩形的边上,另外两个顶点分别在AB、AC上,且长是宽的2倍.则第三个矩形的面积为 ;
(4)按照这样的方式做下去,根据上述计算猜想第四个矩形的面积为 ;第![]() 个矩形的面积为 .
个矩形的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:如图13,等腰△ABC中,底边BC=12,高AD=6.
(1)在△ABC内作矩形EFGH,使F、G在BC上,E、H分别在AB、AC上,且长是宽的2倍.求矩形EFGH的面积.
(2)在(1)的基础上,再作第二个矩形,使其两个顶点在EH上,另外两个顶点分别在AB、AC上,且长是宽的2倍.则第二个矩形的面积为 ;
(3)在(2)的基础上,再作第三个矩形,使其两个顶点在第二个矩形的边上,另外两个顶点分别在AB、AC上,且长是宽的2倍.则第三个矩形的面积为 ;
(4)按照这样的方式做下去,根据上述计算猜想第四个矩形的面积为 ;第![]() 个矩形的面积为 .
个矩形的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
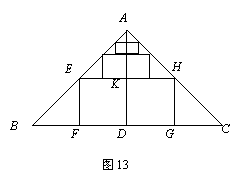
已知:如图13,等腰△ABC中,底边BC=12,高AD=6.
(1)在△ABC内作矩形EFGH,使F、G在BC上,E、H分别在AB、AC上,且长是宽的2倍.求矩形EFGH的面积.
(2)在(1)的基础上,再作第二个矩形,使其两个顶点在EH上,另外两个顶点分别在AB、AC上,且长是宽的2倍.则第二个矩形的面积为 ;
(3)在(2)的基础上,再作第三个矩形,使其两个顶点在第二个矩形的边上,另外两个顶点分别在AB、AC上,且长是宽的2倍.则第三个矩形的面积为 ;
(4)按照这样的方式做下去,根据上述计算猜想第四个矩形的面积为 ;第![]() 个矩形的面积为 .
个矩形的面积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com