Question

【题目】如图，已知⊙O的直径AC与弦BD相交于点F，点E是DB延长线上的一点，∠EAB=∠ADB．

（1）求证：AE是⊙O的切线；
（2）已知点B是EF的中点，求证：△EAF∽△CBA．
（3）已知AF=4，CF=2，在（2）的条件下，求AE的长．

Answer 1

【答案】
（1）

证明：如图1，连接CD，

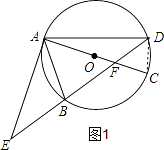
∵AC是⊙O的直径，

∴∠ADC=90°，

∴∠ADB+∠EDC=90°，

∵∠BAC=∠EDC，∠EAB=∠ADB，

∴∠EAC=∠EAB+∠BAC=90°，

∴EA是⊙O的切线．

（2）

证明：如图2，连接BC，

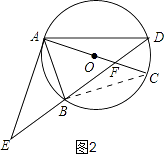
由（1）知，∠EAF=∠EAC=90°，

∵B是EF的中点，

∴在Rt△EAF中，AB=BF（直角三角形斜边的中线等于斜边的一半），

∴∠BAC=∠AFE，

∴△EAF∽△CBA．

（3）

解：∵△EAF∽△CBA，

∴ ，

∵AF=4，CF=2．

∴AC=6，EF=2AB，

∴ ，解得AB=2 ．

∴EF=4 ，

在Rt△AEF中，由勾股定理得，AE= =4

【解析】（1）连接CD，由AC是⊙O的直径，可得出∠ADC=90°，由角的关系可得出∠EAC=90°，即得出EA是⊙O的切线，（2）连接BC，由AC是⊙O的直径，可得出∠ABC=90°，由在Rt△EAF中，B是EF的中点，可得出∠BAC=∠AFE，即可得出△EAF∽△CBA，（3））由△EAF∽△CBA，可得出 ，由比例式可求出AB，由勾股定理得出AE的长．