
【题目】如图,直线y=kx+b(b>0)与抛物线 ![]() 相交于点A(x1 , y1),B(x2 , y2)两点,与x轴正半轴相交于点D,与y轴相交于点C,设△OCD的面积为S,且kS+32=0.
相交于点A(x1 , y1),B(x2 , y2)两点,与x轴正半轴相交于点D,与y轴相交于点C,设△OCD的面积为S,且kS+32=0.
(1)求b的值;
(2)求证:点(y1 , y2)在反比例函数 ![]() 的图象上;
的图象上;
(3)求证:x1OB+y2OA=0.
【答案】
(1)
解:∵直线y=kx+b(b>0)与x轴正半轴相交于点D,与y轴相交于点C,
∴令x=0,得y=b;令y=0,x=﹣ ![]() ,
,
∴△OCD的面积S= ![]() (﹣
(﹣ ![]() )b=﹣
)b=﹣ ![]() .
.
∵kS+32=0,
∴k(﹣ ![]() )+32=0,
)+32=0,
解得b=±8,
∵b>0,
∴b=8;
(2)
证明:由(1)知,直线的解析式为y=kx+8,即x= ![]() ,
,
将x= ![]() 代入y=
代入y= ![]() x2,得y=
x2,得y= ![]() (
( ![]() )2,
)2,
整理,得y2﹣(16+8k2)y+64=0.
∵直线y=kx+8与抛物线 ![]() 相交于点A(x1,y1),B(x2,y2)两点,
相交于点A(x1,y1),B(x2,y2)两点,
∴y1,y2是方程y2﹣(16+8k2)y+64=0的两个根,
∴y1y2=64,
∴点(y1,y2)在反比例函数 ![]() 的图象上
的图象上
(3)
方法一:
证明:由勾股定理,得
OA2= ![]() +
+ ![]() ,OB2=
,OB2= ![]() +
+ ![]() ,AB2=(x1﹣x2)2+(y1﹣y2)2,
,AB2=(x1﹣x2)2+(y1﹣y2)2,
由(2)得y1y2=64,
同理,将y=kx+8代入y= ![]() x2,
x2,
得kx+8= ![]() x2,即x2﹣8kx﹣64=0,
x2,即x2﹣8kx﹣64=0,
∴x1x2=﹣64,
∴AB2= ![]() +
+ ![]() +
+ ![]() +
+ ![]() ﹣2x1x2﹣2y1y2=
﹣2x1x2﹣2y1y2= ![]() +
+ ![]() +
+ ![]() +
+ ![]() ,
,
又∵OA2+OB2= ![]() +
+ ![]() +
+ ![]() +
+ ![]() ,
,
∴OA2+OB2=AB2,
∴△OAB是直角三角形,∠AOB=90°.
如图,过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F.
∵∠AOB=90°,
∴∠AOE=90°﹣∠BOF=∠OBF,
又∵∠AEO=∠OFB=90°,
∴△AEO∽△OFB,
∴ ![]() =
= ![]() ,
,
∵OE=﹣x1,BF=y2,
∴ ![]() =
= ![]() ,
,
∴x1OB+y2OA=0.
方法二:
分别过A,B两点作x轴垂线,垂足分别为E、F,
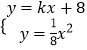 x2﹣8kx﹣64=0,
x2﹣8kx﹣64=0,
∴x1=4k﹣4 ![]() ,x2=4k+
,x2=4k+ ![]() ,
,
y1=4k2+8﹣4k ![]() ,y2=4k2+8+
,y2=4k2+8+ ![]() ,
,
∴A(4k﹣4 ![]() ,4k2+8﹣4k
,4k2+8﹣4k ![]() ),
),
B(4k+ ![]() ,4k2+8+
,4k2+8+ ![]() ),
),
KOA×KOB= ![]() =
= ![]() =﹣1<
=﹣1<
∴OA⊥OB,∠AOE+∠BOF=90°,AE⊥x轴,∠AOE+∠OAE=90°,
∴∠BOF=∠OAE,
∵BF⊥x轴,∴∠AEO=∠BFO=90°,
∴△AEO∽△BFO,
∴ ![]() ,
,
∵OE=﹣x1,BF=y2,
∴x1OB+y2OA=0.
【解析】(1)先求出直线y=kx+b与x轴正半轴交点D的坐标及与y轴交点C的坐标,得到△OCD的面积S=﹣ ![]() ,再根据kS+32=0,及b>0即可求出b的值;(2)先由y=kx+8,得x=
,再根据kS+32=0,及b>0即可求出b的值;(2)先由y=kx+8,得x= ![]() ,再将x=
,再将x= ![]() 代入y=
代入y= ![]() x2 , 整理得y2﹣(16+8k2)y+64=0,然后由已知条件直线y=kx+8与抛物线
x2 , 整理得y2﹣(16+8k2)y+64=0,然后由已知条件直线y=kx+8与抛物线 ![]() 相交于点A(x1 , y1),B(x2 , y2)两点,知y1 , y2是方程y2﹣(16+8k2)y+64=0的两个根,根据一元二次方程根与系数的关系得到y1y2=64,即点(y1 , y2)在反比例函数
相交于点A(x1 , y1),B(x2 , y2)两点,知y1 , y2是方程y2﹣(16+8k2)y+64=0的两个根,根据一元二次方程根与系数的关系得到y1y2=64,即点(y1 , y2)在反比例函数 ![]() 的图象上;(3)先由勾股定理,得出OA2=
的图象上;(3)先由勾股定理,得出OA2= ![]() +
+ ![]() ,OB2=
,OB2= ![]() +
+ ![]() ,AB2=(x1﹣x2)2+(y1﹣y2)2 , 由(2)得y1y2=64,又易得x1x2=﹣64,则OA2+OB2=AB2 , 根据勾股定理的逆定理得出∠AOB=90°.再过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,根据两角对应相等的两三角形相似证明△AEO∽△OFB,由相似三角形对应边成比例得到
,AB2=(x1﹣x2)2+(y1﹣y2)2 , 由(2)得y1y2=64,又易得x1x2=﹣64,则OA2+OB2=AB2 , 根据勾股定理的逆定理得出∠AOB=90°.再过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,根据两角对应相等的两三角形相似证明△AEO∽△OFB,由相似三角形对应边成比例得到 ![]() =
= ![]() ,即可证明x1OB+y2OA=0.
,即可证明x1OB+y2OA=0.
【考点精析】根据题目的已知条件,利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的直径AC与弦BD相交于点F,点E是DB延长线上的一点,∠EAB=∠ADB.
(1)求证:AE是⊙O的切线;
(2)已知点B是EF的中点,求证:△EAF∽△CBA.
(3)已知AF=4,CF=2,在(2)的条件下,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的二次函数y=﹣x2+ax(a>0),点A(n,y1)、B(n+1,y2)、C(n+2,y3)都在这个二次函数的图象上,其中n为正整数.
(1)y1=y2 , 请说明a必为奇数;
(2)设a=11,求使y1≤y2≤y3成立的所有n的值;
(3)对于给定的正实数a,是否存在n,使△ABC是以AC为底边的等腰三角形?如果存在,求n的值(用含a的代数式表示);如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.Rt△ABC内接于⊙O,BC为直径,AB=4,AC=3,D是 ![]() 的中点,CD与AB的交点为E,则
的中点,CD与AB的交点为E,则 ![]() 等于( )
等于( ) 
A.4
B.3.5
C.3
D.2.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的袋子中有四张标着数字1,2,3,4的卡片,小明、小华两人按照各自的规则玩抽卡片游戏. 小明画出树状图如图所示:
小华列出表格如下:
第一次 | 1 | 2 | 3 | 4 |
1 | (1,1) | (2,1) | (3,1) | (4,1) |
2 | (1,2) | (2,2) | ① | (4,2) |
3 | (1,3) | (2,3) | (3,3) | (4,3) |
4 | (1,4) | (2,4) | (3,4) | (4,4) |
回答下列问题:
(1)根据小明画出的树形图分析,他的游戏规则是,随机抽出一张卡片后(填“放回”或“不放回”),再随机抽出一张卡片;
(2)根据小华的游戏规则,表格中①表示的有序数对为;
(3)规定两次抽到的数字之和为奇数的获胜,你认为谁获胜的可能性大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AB=DC,AC与BD相交于P.已知A(2,3),B(1,1),D(4,3),则点P的坐标为( , ). 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于两个相似三角形,如果沿周界按对应点顺序环绕的方向相同,那么称这两个三角形互为顺相似;如果沿周界按对应点顺序环绕的方向相反,那么称这两个三角形互为逆相似.例如,如图①,△ABC∽△A′B′C′,且沿周界ABCA与A′B′C′A′环绕的方向相同,因此△ACB和△A′B′C′互为顺相似;如图②,△ABC∽△A′B′C′,且沿周界ABCA与A′B′C′A′环绕的方向相反,因此△ACB和△A′B′C′互为逆相似.
(1)根据图Ⅰ,图Ⅱ和图Ⅲ满足的条件.可得下列三对相似三角形:①△ADE与△ABC;②△GHO与△KFO;③△NQP与△NMQ;其中,互为顺相似的是;互为逆相似的是 . (填写所有符合要求的序号).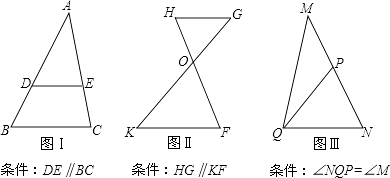

(2)如图③,在锐角△ABC中,∠A<∠B<∠C,点P在△ABC的边上(不与点A,B,C重合).过点P画直线截△ABC,使截得的一个三角形与△ABC互为逆相似.请根据点P的不同位置,探索过点P的截线的情形,画出图形并说明截线满足的条件,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径, ![]() =
= ![]() ,AB=2,连接AC.
,AB=2,连接AC. 
(1)求证:∠CAB=45°;
(2)若直线l为⊙O的切线,C是切点,在直线l上取一点D,使BD=AB,BD所在的直线与AC所在的直线相交于点E,连接AD. (Ⅰ)试探究AE与AD之间的是数量关系,并证明你的结论;
(Ⅱ)是否为定值?若是,请求出这个定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙P的圆心为P(﹣2,1),半径为2,直线MN过点M(2,3),N(4,1). 
(1)请你在图中作出⊙P关于y轴对称的⊙P′(不要求写作法);
(2)请判断(1)中⊙P′与直线MN的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com