
 x2+bx+c经过C,D两点,求抛物线的解析式;
x2+bx+c经过C,D两点,求抛物线的解析式; ,顶点坐标是(-
,顶点坐标是(- ,
, )
)
 x2+bx+c经过C(1,0),D(-2,3),两点代入解析式,解得b、c.(3)当点M在抛物线对称轴的左侧或在抛物线的顶点时,仅当M,E重合时,它们的纵坐标相等,故知道EM不会与x轴平行,设抛物线向上平移H个单位能使EM∥x轴,写出平移后的解析式,根据抛物线的对称性,可知点M的坐标为(2,
x2+bx+c经过C(1,0),D(-2,3),两点代入解析式,解得b、c.(3)当点M在抛物线对称轴的左侧或在抛物线的顶点时,仅当M,E重合时,它们的纵坐标相等,故知道EM不会与x轴平行,设抛物线向上平移H个单位能使EM∥x轴,写出平移后的解析式,根据抛物线的对称性,可知点M的坐标为(2, +h)时,直线EM∥x轴,将点M代入直线y=x+2,解得h.
+h)时,直线EM∥x轴,将点M代入直线y=x+2,解得h. x2+bx+c经过C(1,0),D(-2,3)代入,解得:b=-
x2+bx+c经过C(1,0),D(-2,3)代入,解得:b=- ,c=
,c=
 x2-
x2- x+
x+ ;
;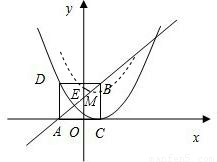 (3)答:存在.
(3)答:存在. (x-1)2+h,
(x-1)2+h, +h),
+h), +h)时,直线EM∥x轴,
+h)时,直线EM∥x轴, +h)代入y=x+2得
+h)代入y=x+2得 +h=2+2
+h=2+2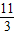 .
.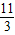 个单位能使EM∥x轴.
个单位能使EM∥x轴.

科目:初中数学 来源:2011年江苏省南通市启东中学中考数学模拟试卷(一)(解析版) 题型:解答题
 x2+bx+c经过C,D两点,求抛物线的解析式;
x2+bx+c经过C,D两点,求抛物线的解析式; ,顶点坐标是(-
,顶点坐标是(- ,
, )
)
查看答案和解析>>
科目:初中数学 来源:2010年福建省南平市中考数学试卷(解析版) 题型:解答题
 x2+bx+c经过C,D两点,求抛物线的解析式;
x2+bx+c经过C,D两点,求抛物线的解析式; ,顶点坐标是(-
,顶点坐标是(- ,
, )
)
查看答案和解析>>
科目:初中数学 来源:2010年福建省南平市中考数学试卷(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com