
ЎѕМвДїЎїОЄ№ДАшѕУГсЅЪФјУГµзЈ¬ДіКРІЙУГјЫёсµчїШКЦ¶ОґпµЅКЎµзДїµД.ёГКРµз·СКХ·С±кЧјИзПВ±н(°ґФВЅбЛг) :
ГїФВУГµзБї/¶И | µзјЫ/(ФЄ/¶И) |
І»і¬№э |
|
і¬№э |
|
і¬№э |
|
ЅвґрПВБРОКМв:
ЈЁ1Ј©ДіѕУГс![]() ФВ·ЭУГµзБїОЄ
ФВ·ЭУГµзБїОЄ![]() ¶ИЈ¬ЗлОКёГѕУГс
¶ИЈ¬ЗлОКёГѕУГс![]() ФВУ¦ЅЙµз·С¶аЙЩФЄЈї
ФВУ¦ЅЙµз·С¶аЙЩФЄЈї
ЈЁ2Ј©ЙиДіФВµДУГµзБїОЄ![]() ¶И
¶И![]() Ј¬КФРґіцІ»Н¬УГµзБї·¶О§У¦ЅЙµДµз·С(УГ
Ј¬КФРґіцІ»Н¬УГµзБї·¶О§У¦ЅЙµДµз·С(УГ![]() ±нКѕ) .
±нКѕ) .
ЈЁ3Ј©ДіѕУГс![]() ФВ·ЭЅЙµз·С
ФВ·ЭЅЙµз·С![]() ФЄЈ¬ЗуёГѕУГс
ФЄЈ¬ЗуёГѕУГс![]() ФВ·ЭµДУГµзБї.
ФВ·ЭµДУГµзБї.
Ўѕґр°ёЎїЈЁ1Ј©![]() ФЄЈ»ЈЁ2Ј©µ±
ФЄЈ»ЈЁ2Ј©µ±![]() К±Ј¬У¦ё¶µз·С
К±Ј¬У¦ё¶µз·С![]() ФЄ;µ±
ФЄ;µ±![]() К±Ј¬У¦ё¶µз·С
К±Ј¬У¦ё¶µз·С![]() ФЄ;µ±
ФЄ;µ±![]() К±Ј¬У¦ё¶µз·С
К±Ј¬У¦ё¶µз·С![]() ФЄ.ЈЁ3Ј©
ФЄ.ЈЁ3Ј©![]() ¶И.
¶И.
ЎѕЅвОцЎї
ЈЁ1Ј©ёщѕЭУГµзБїАаРН·Ц±рЅшРРјЖЛгјґїЙЈ»
ЈЁ2Ј©·ЦИэЦЦЗйїцЅшРРМЦВЫЈ¬µ±xІ»і¬№э150¶ИК±Ј¬xі¬№э150¶ИЈ¬µ«І»і¬№эК±250¶ИК±єНaі¬№э250¶ИК±Ј¬ФЩ·Ц±рґъИлјЖЛгјґїЙЈ®
ЈЁ3Ј©ТтОЄ![]() Ј¬ЛщТФёГѕУГс
Ј¬ЛщТФёГѕУГс![]() ·ЭµДУГµзБїі¬№э
·ЭµДУГµзБїі¬№э![]() ¶ИЈ¬ѕЭґЛБР·ЅіМЗуЅвјґїЙ.
¶ИЈ¬ѕЭґЛБР·ЅіМЗуЅвјґїЙ.
ЈЁ1Ј©УЙМвТвЈ¬µГ![]() (ФЄ).
(ФЄ).
јґёГѕУГс12ФВУ¦ЅЙЅ»µз·С94.5ФЄ.
ЈЁ2Ј©ИфДі»§µДУГµзБїОЄ![]() ¶ИЈ¬Фт
¶ИЈ¬Фт
µ±![]() К±Ј¬У¦ё¶µз·С
К±Ј¬У¦ё¶µз·С![]() ФЄ;
ФЄ;
µ±![]() К±Ј¬У¦ё¶µз·С
К±Ј¬У¦ё¶µз·С![]() ФЄ;
ФЄ;
µ±![]() К±Ј¬У¦ё¶µз·С
К±Ј¬У¦ё¶µз·С![]() ФЄ.
ФЄ.
ЈЁ3Ј©ТтОЄ![]() Ј¬ЛщТФёГѕУГс
Ј¬ЛщТФёГѕУГс![]() ·ЭµДУГµзБїі¬№э
·ЭµДУГµзБїі¬№э![]() ¶И.
¶И.
УЙЈЁ2Ј©µГ:![]() Ј¬
Ј¬
ЅвµГ![]() .
.
ґр:ёГѕУГс![]() ·ЭµДУГµзБїОЄ
·ЭµДУГµзБїОЄ![]() ¶И.
¶И.


 їЪЛгРДЛгЛЩЛгУ¦УГМвПµБРґр°ё
їЪЛгРДЛгЛЩЛгУ¦УГМвПµБРґр°ё Н¬ІЅНШХ№ФД¶БПµБРґр°ё
Н¬ІЅНШХ№ФД¶БПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ЎчABCЦРЈ¬ЎПACBµДЖЅ·ЦПЯЅ»ABУЪµгDЈ¬ЧчCDµДґ№Ц±ЖЅ·ЦПЯЈ¬·Ц±рЅ»ACЎўDCЎўBCУЪµгEЎўGЎўFЈ¬Б¬ЅУDEЎўDFЈ®
ЈЁ1Ј©ЗуЦ¤ЈєЛД±ЯРОDFCEКЗБвРОЈ»
ЈЁ2Ј©ИфЎПABC=60Ј¬ЎПACB=45ЎгЈ¬BD=2Ј¬КФЗуBFµДі¤Ј®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
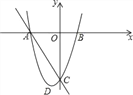
ЎѕМвДїЎїИзНјЈ¬ЕЧОпПЯµДНјПуУлxЦбЅ»УЪAЎўBБЅµгЈ¬µгAФЪµгBµДЧу±ЯЈ¬УлyЦбЅ»УЪµгCЈ¬µгDКЗЕЧОпПЯµД¶ҐµгЈ¬ЗТAЈЁ©Ѓ6Ј¬0Ј©Ј¬DЈЁ©Ѓ2Ј¬©Ѓ8Ј©Ј®
ЈЁ1Ј©ЗуЕЧОпПЯµДЅвОцКЅЈ»
ЈЁ2Ј©µгPКЗЦ±ПЯACПВ·ЅµДЕЧОпПЯЙПТ»¶ЇµгЈ¬І»УлµгAЎўCЦШєПЈ¬Зу№эµгPЧчxЦбµДґ№ПЯЅ»УЪACУЪµгEЈ¬ЗуПЯ¶ОPEµДЧоґуЦµј°PµгЧш±кЈ»
ЈЁ3Ј©ФЪЕЧОпПЯµД¶ФіЖЦбЙПЧг·сґжФЪµгMЈ¬К№µГЎчACMОЄЦ±ЅЗИэЅЗРОЈїИфґжФЪЈ¬ЗуіцµгMµДЧш±кЈ»ИфІ»ґжФЪЈ¬ЗлЛµГчАнУЙЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
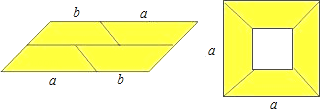
ЎѕМвДїЎїЈЁ1Ј©±ИЅПЧуЎўУТБЅНјµДТхУ°Ії·ЦГж»эЈ¬їЙТФµГµЅіЛ·Ё№«КЅЎЎ_________ЎЎЈЁУГКЅЧУ±нґпЈ©Ј®
ЈЁ2Ј©ФЛУГДгЛщµГµЅµД№«КЅЈ¬јЖЛгЈЁa+2b©ЃcЈ©ЈЁa©Ѓ2b©ЃcЈ©Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ТФЦ±ПЯABЙПТ»µгOОЄ¶ЛµгЧчЙдПЯOCЈ¬К№ЎПAOCЈЅ65ЎгЈ¬Ѕ«Т»ёцЦ±ЅЗИэЅЗРОµДЦ±ЅЗ¶Ґµг·ЕФЪµгOґ¦Ј®ЈЁЧўЈєЎПDOEЈЅ90ЎгЈ©
ЈЁ1Ј©ИзНјўЩЈ¬ИфЦ±ЅЗИэЅЗ°еDOEµДТ»±ЯOD·ЕФЪЙдПЯOAЙПЈ¬ФтЎПCOEЈЅЎЎ ЎЎЈ»
ЈЁ2Ј©ИзНјўЪЈ¬Ѕ«Ц±ЅЗИэЅЗ°еDOEИЖµгOЛіК±Хл·ЅПтЧЄ¶ЇµЅДіёцО»ЦГЈ¬ИфOCЗЎєГЖЅ·ЦЎПAOEЈ¬ЗуЎПCODµД¶ИКэЈ»
ЈЁ3Ј©ИзНјўЫЈ¬Ѕ«Ц±ЅЗИэЅЗ°еDOEИЖµгOИОТвЧЄ¶ЇЈ¬Из№ыODКјЦХФЪЎПAOCµДДЪІїЈ¬КФІВПлЎПAODєНЎПCOEУРФхСщµДКэБї№ШПµЈїІўЛµГчАнУЙЈ®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТ»ёцЕъ·ўЙМПъКЫіЙ±ѕОЄ20ФЄ/З§їЛµДДіІъЖ·Ј¬ёщѕЭОпјЫІїГЕ№ж¶ЁЈєёГІъЖ·ГїЗ§їЛКЫјЫІ»µГі¬№э90ФЄЈ¬ФЪПъКЫ№эіМЦР·ўПЦµДКЫБїyЈЁЗ§їЛЈ©УлКЫјЫxЈЁФЄ/З§їЛЈ©ВъЧгТ»ґОєЇКэ№ШПµЈ¬¶ФУ¦№ШПµИзПВ±нЈє
КЫјЫxЈЁФЄ/З§їЛЈ© | Ў | 50 | 60 | 70 | 80 | Ў |
ПъКЫБїyЈЁЗ§їЛЈ© | Ў | 100 | 90 | 80 | 70 | Ў |
ЈЁ1Ј©ЗуyУлxµДєЇКэ№ШПµКЅЈ»
ЈЁ2Ј©ёГЕъ·ўЙМИфПл»сµГ4000ФЄµДАыИуЈ¬У¦Ѕ«КЫјЫ¶ЁОЄ¶аЙЩФЄЈї
ЈЁ3Ј©ёГІъЖ·ГїЗ§їЛКЫјЫОЄ¶аЙЩФЄК±Ј¬Еъ·ўЙМ»сµГµДАыИуwЈЁФЄЈ©ЧоґуЈїґЛК±µДЧоґуАыИуОЄ¶аЙЩФЄЈї
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄЈ¬ЎчABCЦРЈ¬ЎПACB=90ЎгЈ¬AC=BCЈ¬µгEКЗBCЙПТ»µгЈ¬Б¬ЅУAEЈ®
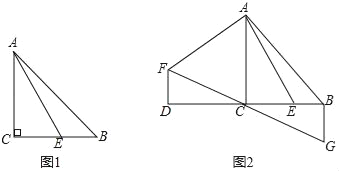
ЈЁ1Ј©ИзНј1Ј¬µ±ЎПBAE=15ЎгЈ¬CE=![]() К±Ј¬ЗуABµДі¤Ј®
К±Ј¬ЗуABµДі¤Ј®
ЈЁ2Ј©ИзНј2Ј¬СУі¤BCЦБDЈ¬К№DC=BCЈ¬Ѕ«ПЯ¶ОAEИЖµгAЛіК±ХлРэЧЄ90ЎгµГПЯ¶ОAFЈ¬Б¬ЅУDFЈ¬№эµгBЧчBGЎНBCЈ¬Ѕ»FCµДСУі¤ПЯУЪµгGЈ¬ЗуЦ¤ЈєBG=BEЈ®
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com