
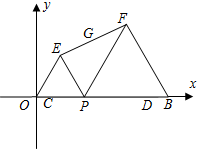
 如图,C、D、B的坐标分别为(1,0)(9,0)(10,0),点P(t,0)是CD上一个动点,在x轴上方作等边△OPE和△BPF,连EF,G为EF的中点.
如图,C、D、B的坐标分别为(1,0)(9,0)(10,0),点P(t,0)是CD上一个动点,在x轴上方作等边△OPE和△BPF,连EF,G为EF的中点. 过点G,当PG=
过点G,当PG=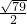 时,则k=______.
时,则k=______.
 OP,FN=
OP,FN= PB,
PB, t=
t= (10-t),
(10-t), (EM+FN)=
(EM+FN)= [
[ t+
t+ (10-t)]=
(10-t)]= ,HM=
,HM= MN=
MN= (ON-OM)=
(ON-OM)= [t+
[t+ (10-t)-
(10-t)- t]=
t]= ,
, -
- t或
t或 t-
t- ,
, )2+(
)2+(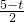 )2=(
)2=(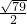 )2,
)2, +
+ t=4,
t=4, ),
), )代入y=
)代入y= 得k=4×
得k=4× =10
=10 ;
; +
+ =6,
=6, ),
), )代入y=
)代入y= 得k=6×
得k=6× =15
=15 ;
; 或15
或15 .
. 或15
或15 .
. OP,FN=
OP,FN= PB,所以EM=FN时,EF∥OB,则
PB,所以EM=FN时,EF∥OB,则 t=
t= (10-t),然后即方程即可得到t的值;
(10-t),然后即方程即可得到t的值; (EM+FN)=
(EM+FN)= ,HM=
,HM= MN=
MN= (ON-OM)=
(ON-OM)= ,得到PH=
,得到PH= -
- t或
t或 t-
t- ,
, )2+(
)2+(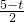 )2=(
)2=(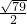 )2,解得t1=3,t2=7,然后分别确定G点坐标,再代入反比例函数解析式可得到k的值.,
)2,解得t1=3,t2=7,然后分别确定G点坐标,再代入反比例函数解析式可得到k的值.,

 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
| k |
| x |
| k |
| x |
| 10 |
| 7 |

查看答案和解析>>
科目:初中数学 来源: 题型:
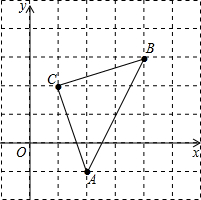 如图,直角坐标系中,△ABC的顶点都在网格点上,其中C点坐(1,2)
如图,直角坐标系中,△ABC的顶点都在网格点上,其中C点坐(1,2)查看答案和解析>>
科目:初中数学 来源:2010-2011学年广东省深圳市宝安区九年级第三次调研测试数学 题型:选择题
如图,在方格纸上建立的平面直角坐标系中,将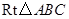 绕点
绕点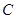 按顺时针方向旋转
按顺时针方向旋转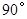 ,得到
,得到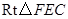 ,则点
,则点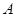 的对应点
的对应点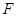 的坐 标是
的坐 标是
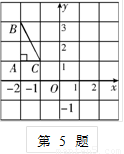
A.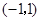 B.
B.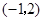 C.
C.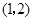 D.
D.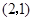
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com