
分析 根据二次项系数非负、根的判别式△≥0以及被开方数非负,即可得出关于m的一元一次不等式组,解之即可得出结论.
解答 解:∵关于x的一元二次方程(m-1)x2+$\sqrt{m}$x+1=0有实数根,
∴$\left\{\begin{array}{l}{m-1≠0}\\{△=(\sqrt{m})^{2}-4(m-1)≥0}\\{m≥0}\end{array}\right.$,
解得:0≤m≤$\frac{4}{3}$且m≠1.
故答案为:0≤m≤$\frac{4}{3}$且m≠1.
点评 本题考查了根的判别式以及解一元一次不等式组,由二次项系数非负、根的判别式△≥0以及被开方数非负,列出关于m的一元一次不等式组是解题的关键.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:解答题
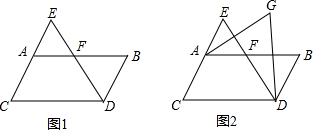
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
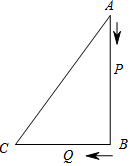 如图,已知△ABC中,∠B=90°,AB=12cm,BC=9cm,P,Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
如图,已知△ABC中,∠B=90°,AB=12cm,BC=9cm,P,Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
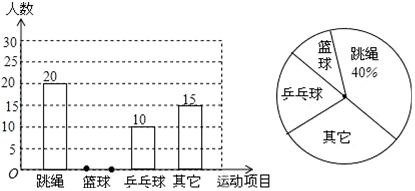
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x (单位:元) | 实际在甲超市的花费 (单位:元) | 实际在乙超市的花费 (单位:元) |
| 0<x≤200 | x | x |
| 200<x≤300 | 200+(x-200)×95%(或10+0.95x) | x |
| x>300 | 200+(x-200)×95%(或10+0.95x) | 300+(x-300)×90%(或30+0.9x) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
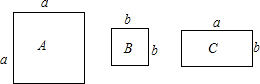
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com