
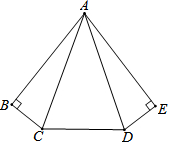
 已知五边形ABCDE中,∠B=∠E=90°,AB=AE,AC=AD,∠BCD=140°.
已知五边形ABCDE中,∠B=∠E=90°,AB=AE,AC=AD,∠BCD=140°.分析 (1)首先证明Rt△ACB≌Rt△ADE(HL),推出∠ACB=∠ADE,由AC=AD,推出∠ACD=∠ADC即可证明.
(2)求出∠CDE的度数,利用五边形内角和公式,即可解决问题.
解答 证明:(1)在Rt△ACB和Rt△ADE中,
$\left\{\begin{array}{l}{AC=AD}\\{AB=AE}\end{array}\right.$,
∴Rt△ACB≌Rt△ADE(HL),
∠ACB=∠ADE(全等三角形的对应角相等).
(2)∵AC=AD,
∴∠ACD=∠ADC,
∵∠ACB=∠ADE,
∴∠BCD=∠CDE=140°,
∵∠B=∠E=90°,
∴∠BAE=(5-2)×180°-90°-90°-140°-140°=80°.
点评 本题考查全等三角形的判定和性质、等腰三角形的性质、多边形的内角和公式等知识,解题的关键是正确寻找全等三角形解决问题,会用五边形内角和公式,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
| 会员年卡类型 | 办卡费用(元) | 每次游泳收费(元) |
| A类 | 100 | 30 |
| B类 | 200 | 25 |
| C类 | 500 | 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知⊙O是锐角△ABC的外接圆,BE,CF分别是AC,AB边上的高,自垂足E,F分别作AB,AC的垂线,垂足为G,H,设EG与FH相交于K.
如图,已知⊙O是锐角△ABC的外接圆,BE,CF分别是AC,AB边上的高,自垂足E,F分别作AB,AC的垂线,垂足为G,H,设EG与FH相交于K.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
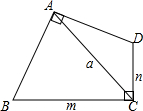 如图,四边形ABCD中,∠A=∠C=90°,AB=AD,BC=m,CD=n,对角线AC=a,则m,n,a满足的数量关系是m+n=$\sqrt{2}$a.
如图,四边形ABCD中,∠A=∠C=90°,AB=AD,BC=m,CD=n,对角线AC=a,则m,n,a满足的数量关系是m+n=$\sqrt{2}$a.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某商场出售一批进价为每个2元的笔记本,在市场营销中发现此商品的日销售单价x(元)与日销售量y(个)之间有如下关系:
某商场出售一批进价为每个2元的笔记本,在市场营销中发现此商品的日销售单价x(元)与日销售量y(个)之间有如下关系:| x(元) | 3 | 4 | 5 | 6 |
| y(个) | 20 | 15 | 12 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com