
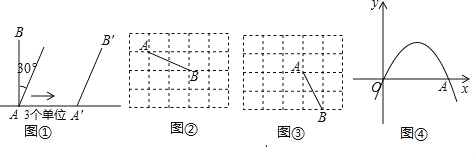
【题目】定义:以线段l的一个端点为旋转中心,将这条线段顺时针旋转α(0°<α≤360°),再沿水平方向向右平移m个单位后得到对应线段l′(若m<0,则表示沿水平向左的方向平移|m|个单位),则将线段l到线段l′的变换记为<α,m>.如图①,将线段AB绕点A顺时针旋转30°,再沿水平向右的方向平移3个单位后得到线段A′B′的变换记为<30°,3>.
(1)已知:图②、图③均为5×4的正方形网格,在图②中将线段AB绕点A进行变换<90°,4>,得到对应线段A′B′;在图③中将线段AB绕点A进行变换<270°,﹣3>,得到对应线段A′B′,按要求分别画出变换后的对应线段.
(2)如图④,在平面直角坐标系中,抛物线y=﹣![]() x2+2x与x轴正半轴交于点A,线段OA绕点A进行变换<α,m>后得到对应线段的一个端点恰好落在抛物线的顶点处,直接写出符合题意的<α,m>为________________________________.
x2+2x与x轴正半轴交于点A,线段OA绕点A进行变换<α,m>后得到对应线段的一个端点恰好落在抛物线的顶点处,直接写出符合题意的<α,m>为________________________________.
【答案】(1)作图见解析;(2)<30°,![]() >或<150°,
>或<150°,![]() >.
>.
【解析】
![]() 利用新定义直接作出图形;
利用新定义直接作出图形;
![]() 先确定出点A的坐标,抛物线的顶点坐标,再判断出线段OA绕点A顺时针旋转使点O的对应点落在直线l上,分两种情况分别讨论求得
先确定出点A的坐标,抛物线的顶点坐标,再判断出线段OA绕点A顺时针旋转使点O的对应点落在直线l上,分两种情况分别讨论求得
(1)①如图②所示,A'B'为所求作的线段,
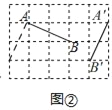
②如图③所示,A'B'为所求作的线段,
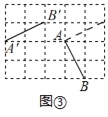
(2)![]()
∴此抛物线的顶点E坐标为(2,2),
![]()
![]()
∴x=0或x=4,
∴A(4,0),
∴OA=4,
过E作直线l∥x轴,
由平移知,OA绕点A顺时针旋转,点O的对应点落在直线l上,如图④中点D或F,
①当点O的对应点落在D点时,过点D作DP⊥x轴,
∴DP=2,
在Rt△APD中,AD=OA=4,
![]()
![]()
![]()
![]()
![]()
∴<α,m>为<30°,![]() >,
>,
②当点O的对应点落在点F处时,
同①的方法得,<α,m>为<150°,![]() >,
>,
故答案为<30°,![]() >或<150°,
>或<150°,![]() >.
>.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某书店老板去图书批发市场购买某种图书,第一次用![]() 元购书若干本, 并按该书定价
元购书若干本, 并按该书定价![]() 元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了
元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了![]() ,他用
,他用![]() 元所购该书数量比第一次多
元所购该书数量比第一次多![]() 本.当按定价
本.当按定价![]() 元售出
元售出![]() 本时,出现滞销,便以定价的
本时,出现滞销,便以定价的![]() 折售完剩余的书.
折售完剩余的书.
![]() 每本书第一次的批发价是多少钱?
每本书第一次的批发价是多少钱?
![]() 试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?若赚钱,赚多少?
试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?若赚钱,赚多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x22(k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB,AC的长是方程的两个实数根,第三边BC的长为5.当△ABC是等腰三角形时,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 边上的高,
边上的高,![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 的中点.
的中点.

(1)求证:![]() ;
;
(2)联结![]() 、
、![]() ,猜想
,猜想![]() 与
与![]() 之间的关系,并写出推理过程;
之间的关系,并写出推理过程;
(3)若将锐角![]() 变为钝角
变为钝角![]() ,如图(2),上述(1)(2)中的结论是否都成立?若结论成立,直接回答,不需证明;若结论不成立,说明理由.
,如图(2),上述(1)(2)中的结论是否都成立?若结论成立,直接回答,不需证明;若结论不成立,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线a,b,c表示交叉的三条公路,现要建一货物中转站,要求它到这三条公路的距离相等,则可供选择的站址最多有![]()
![]()

A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】寒假即将到来,外出旅游的人数逐渐增多,对旅行包的需求也将增多,某店准备到生产厂家购买旅行包,该厂有甲、乙两种新型旅行包.若购进10个甲种旅行包和20个乙种旅行包共需5600元,若购进20个甲种旅行包和10个乙种旅行包共需5200元.
(1)甲、乙两种旅行包的进价分别是多少元?
(2)若该店恰好用了7000元购买旅行包;
①设该店购买了m个甲种旅行包,求该店购买乙种旅行包的个数;
②若该店将甲种旅行包的售价定为298元,乙种旅行包的售价定为325元,则当该店怎么样进货,才能获得最大利润,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,AB=4,D是BC的中点,将△ABD绕点A旋转后得到△ACE,连接DE交AC于点F,则△AEF的面积为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,在
,在![]() 的外部作等边三角形
的外部作等边三角形![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)如图1,若![]() ,求
,求![]() 的度数;
的度数;
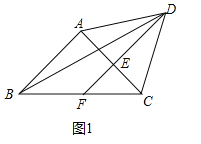
(2)如图2,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
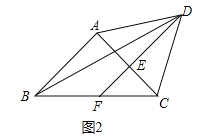
①补全图2;
②若![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
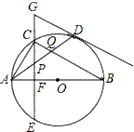
【题目】如图,在⊙O中,AB是⊙O的直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点F,过点D的切线交EC的延长线于点G,连接AD,分别交CF、BC于点P、Q,连接AC.给出下列结论:①GP=GD;②∠BAD=∠ABC;③点P是△ACQ的外心;④![]() .其中正确的是______________(填序号)
.其中正确的是______________(填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com