
【题目】寒假即将到来,外出旅游的人数逐渐增多,对旅行包的需求也将增多,某店准备到生产厂家购买旅行包,该厂有甲、乙两种新型旅行包.若购进10个甲种旅行包和20个乙种旅行包共需5600元,若购进20个甲种旅行包和10个乙种旅行包共需5200元.
(1)甲、乙两种旅行包的进价分别是多少元?
(2)若该店恰好用了7000元购买旅行包;
①设该店购买了m个甲种旅行包,求该店购买乙种旅行包的个数;
②若该店将甲种旅行包的售价定为298元,乙种旅行包的售价定为325元,则当该店怎么样进货,才能获得最大利润,并求出最大利润.
【答案】(1) 甲、乙两种旅行包的进价分别是160元,200元;(2)①![]() 个;②设购进甲种旅行包40个,乙种旅行包3个时, 能获得最大利润,最大利润是5895元.
个;②设购进甲种旅行包40个,乙种旅行包3个时, 能获得最大利润,最大利润是5895元.
【解析】
(1)设甲种旅行包每件进价是x元,乙种旅行包每件进价是y元,根据“购进10个甲种旅行包和20个乙种旅行包共需5600元,若购进20个甲种旅行包和10个乙种旅行包共需5200元”列出方程组解答即可;
(2)设购进甲种旅行包m个,则乙种旅行包![]() 个,根据利润=售价﹣进价、甲乙旅行包的数量都是正整数解答即可.
个,根据利润=售价﹣进价、甲乙旅行包的数量都是正整数解答即可.
解:(1)设甲种旅行包每个进价是x元,乙种旅行包每个进价是y元,可得:
![]() ,解得
,解得![]() ,
,
答:甲、乙两种旅行包的进价分别是160元,200元;
(2)①设购进甲种旅行包m个,则乙种旅行包![]() 个;
个;
②设购进甲种旅行包m个,则乙种旅行包![]() 个,因为m的值和
个,因为m的值和![]() 都是正整数,所以m=5,10,15,20,25,30,35,40.
都是正整数,所以m=5,10,15,20,25,30,35,40.
可得:w=(298﹣160)m+(325﹣200)×![]() =38m+4375,因为k=38>0,所以w的值随着m的增大而增大,∴当m=40时,
=38m+4375,因为k=38>0,所以w的值随着m的增大而增大,∴当m=40时,![]() =3时,能获得最大利润,最大利润是5895元.
=3时,能获得最大利润,最大利润是5895元.


科目:初中数学 来源: 题型:
【题目】如图,A、B、C是正方形网格中的三个格点.
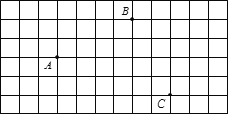
(1)①画射线AC;
②画线段BC;
③过点B画AC的平行线BD;
④在射线AC上取一点E,画线段BE,使其长度表示点B到AC的距离;
(2)在(1)所画图中,
①BD与BE的位置关系为 ;
②线段BE与BC的大小关系为BE BC(填“>”、“<”或“=”),理由是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组做“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了如图所示的折线统计图,则符合这一结果的试验最有可能的是( )

A. 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B. 一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
C. 暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球
D. 掷一个质地均匀的正六面体骰子,向上的面点数是4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件.已知生产一件A种产品需用甲种原料9千克、乙种原料3千克,可获利润700元;生产一件B种产品需用甲种原料4千克、乙种原料10千克,可获利润1200元。设生产A种产品的生产件数为x, A、B两种产品所获总利润为y (元)
(1)试写出y与x之间的函数关系式;
(2)求出自变量x的取值范围;
(3)利用函数的性质说明哪种生产方案获总利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
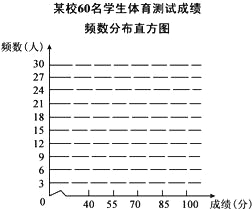
【题目】某校为了更好的开展“学校特色体育教育”,从全校八年级的各班分别随机抽取了5名男生和5名女生,组成了一个容量为60的样本,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:某校60名学生体育测试成绩频数分布表
成绩 | 划记 | 频数 | 百分比 |
优秀 | 正正正 | a | 30% |
良好 | 正正正正正正 | 30 | b |
合格 | 正 | 9 | 15% |
不合格 |
| 3 | 5% |
合计 | 60 | 60 | 100% |
(说明:40﹣﹣﹣55分为不合格,55﹣﹣﹣70分为合格,70﹣﹣﹣85分为良好,85﹣﹣﹣100分为优秀)请根据以上信息,解答下列问题:
(1)表中的a=_____,b=_____;
(2)请根据频数分布表,画出相应的频数分布直方图;
(3)如果该校八年级共有150名学生,根据以上数据,估计该校八年级学生身体素质良好及以上的人数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(-3,0)、B(1,0)、C(0,3)三点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线,垂足点为E,连接AE.
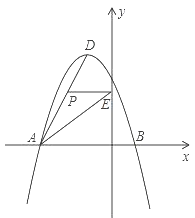
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如果P点的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值;
(3)在(2)的条件下,当S取到最大值时,过点P作x轴的垂线,垂足为F,连接EF,把△PEF沿直线EF折叠,点P的对应点为点P′,求出P′的坐标,并判断P′是否在该抛物线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4,则以下四个结论中: ①△BDE是等边三角形; ②AE∥BC; ③△ADE的周长是9; ④∠ADE=∠BDC.其中正确的序号是( )
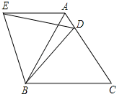
A.②③④B.①②④C.①②③D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
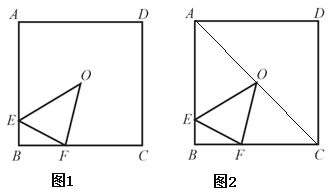
【题目】如图1,点O为正方形ABCD 的中心,E为AB 边上一点,F为BC边上一点,△EBF的周长等于 BC 的长.
(1)求∠EOF 的度数.
(2)连接 OA、OC(如图2).求证:△AOE∽△CFO.
(3)若OE=![]() OF,求
OF,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发部某一玩具价格如图所示,现有甲、乙两个商店,计划在“六一”儿童节前到该批发部购买此类玩具.两商店所需玩具总数为120个,乙商店所需数量不超过50个,设甲商店购买![]() 个.如果甲、乙两商店分别购买玩具,两商店需付款总和为y元.
个.如果甲、乙两商店分别购买玩具,两商店需付款总和为y元.
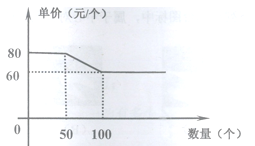
(1)求y关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)若甲商店购买不超过100个,请说明甲、乙两商店联合购买比分别购买最多可节约多少钱;
(3)“六一”儿童节之后,该批发部对此玩具价格作了如下调整:数量不超过100个时,价格不变;数量超过100个时,每个玩具降价a元.在(2)的条件下,若甲、乙两商店“六一”儿童节之后去批发玩具,最多可节约2800元,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com