
【题目】如图,A、B、C是正方形网格中的三个格点.
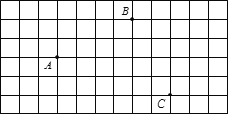
(1)①画射线AC;
②画线段BC;
③过点B画AC的平行线BD;
④在射线AC上取一点E,画线段BE,使其长度表示点B到AC的距离;
(2)在(1)所画图中,
①BD与BE的位置关系为 ;
②线段BE与BC的大小关系为BE BC(填“>”、“<”或“=”),理由是 .
【答案】(1)①答案见解析;②答案见解析;③答案见解析;④答案见解析;(2)①垂直;②<,垂线段最短.
【解析】
(1)①画射线AC即可;
②画线段BC即可;
③过点B作AC的平行线BD即可;
④过B作BE⊥AC于E即可;
(2)①根据平行线的性质得到BD⊥BE;
②根据垂线段最短即可得出结论.
(1)①如图所示,射线AC就是所求图形;
②如图所示,线段BC就是所求图形;
③如图所示,直线BD就是所求图形;
④如图所示,线段BE就是所求图形.
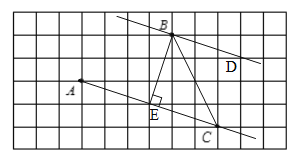
(2)①∵BD∥AC,∠BEC=90°,
∴∠DBE=180°-∠BEC=180°-90°=90°,
∴BD⊥BE.
故答案为:垂直.
②∵BE⊥AC,
∴BE<BC.理由如下:
垂线段最短.
故答案为:<,垂线段最短.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】在平整的地面上,有若干个完全相同的棱长为![]() 的小正方体堆成一个几何体,如下图所示.
的小正方体堆成一个几何体,如下图所示.
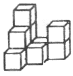



(1)该几何体是由 个小正方体组成,请画出它的主视图、左视图、俯视图(网格中所画的图形要画出各个正方形边框并涂上阴影).
(2)如果在这个几何体露在外面的表面喷上黄色的漆,每平方厘米用2克,则共需 克漆.
(3)这个几何体上,再添加一些相同的小正方体并保持这个几何体的俯视图和左视图不变,那么最多可以再添加 个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】首先,我们学习一道“最值”问题的解答:
问题:已知x>0,求![]() 的最小值.
的最小值.
解答:对于x>0,我们有: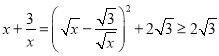
当![]() ,即
,即![]() 时,上述不等式取等号,所以
时,上述不等式取等号,所以![]() 的最小值是
的最小值是![]()
由解答知,![]() 的最小值是
的最小值是![]() .
.
弄清上述问题及解答方法之后,解答下述问题:
(1)求![]() 的最小值.
的最小值.
(2)在直角坐标系 xOy 中,一次函数![]() 的图象与 x 轴、 y 轴分别交于 A 、 B 两点.
的图象与 x 轴、 y 轴分别交于 A 、 B 两点.
①求 A 、 B 两点的坐标;
②求当OAB 的面积值等于![]() 时,用b 表示 k ;
时,用b 表示 k ;
③在②的条件下,求AOB 面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,则Sn=____.(用含n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂甲、乙两人加工同一种零件,每小时甲比乙多加工10个这种零件,甲加工150个这种零件所用的时间与乙加工120个这种零件所用的时间相等,
(1)甲、乙两人每小时各加工多少个这种零件?
(2)该工厂计划加工920个零件,甲参与加工这批零件不超过12天,则乙至少加工多少天才能加工完这批零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
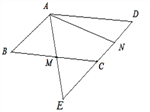
【题目】如图,在平行四边形ABCD中,M,N分别为BC,CD的中点,AM=1,AN=2,∠MAN=60°,AM ,DC的延长线相交于点E,则AB的长为_____________;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某加工厂购进甲、乙两种原料,若甲原料的单价为![]() 元
元![]() 千克,乙原料的单价为
千克,乙原料的单价为![]() 元
元![]() 千克.现该工厂预计用不多于
千克.现该工厂预计用不多于![]() 万元且不少于
万元且不少于![]() 万元的资金购进这两种原料共
万元的资金购进这两种原料共![]() 千克.
千克.
(l)若需购进甲原料![]() 千克,请求出
千克,请求出![]() 的取值范围;
的取值范围;
(2)经加工后:甲原料加工的产品,利润率为![]() ;每一千克乙原料加工的产品售价为
;每一千克乙原料加工的产品售价为![]() 元.则应该怎样安排进货,才能使销售的利润最大?
元.则应该怎样安排进货,才能使销售的利润最大?
(3)在(2)的条件下,为了促销,公司决定每售出一千克乙原料加工的产品,返还顾客现金![]() 元,而甲原料加工的产品售价不变,要使所有进货方案获利相同,求
元,而甲原料加工的产品售价不变,要使所有进货方案获利相同,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台.若商店保持两种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】寒假即将到来,外出旅游的人数逐渐增多,对旅行包的需求也将增多,某店准备到生产厂家购买旅行包,该厂有甲、乙两种新型旅行包.若购进10个甲种旅行包和20个乙种旅行包共需5600元,若购进20个甲种旅行包和10个乙种旅行包共需5200元.
(1)甲、乙两种旅行包的进价分别是多少元?
(2)若该店恰好用了7000元购买旅行包;
①设该店购买了m个甲种旅行包,求该店购买乙种旅行包的个数;
②若该店将甲种旅行包的售价定为298元,乙种旅行包的售价定为325元,则当该店怎么样进货,才能获得最大利润,并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com