
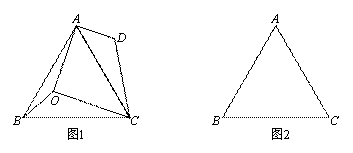
已知,点O是等边△ABC内的任一点,连接OA,OB,OC.
(1) 如图1,已知∠AOB=150°,∠BOC=120°,将△BOC绕点C按顺时针方向旋转60°得△ADC.
①∠DAO的度数是 ;
②用等式表示线段OA,OB,OC之间的数量关系,并证明;
(2) 设∠AOB=α,∠BOC=β.
①当α,β满足什么关系时,OA+OB+OC有最小值?请在图2中画出符合条件的图形,并说明理由;
②若等边△ABC的边长为1,直接写出OA+OB+OC的最小值.
解:(1)①90°.
②线段OA,OB,OC之间的数量关系是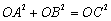 .
.
如图1,连接OD.
∵△BOC绕点C按顺时针方向旋转60°得△ADC,
 ∴△ADC≌△BOC,∠OCD=60°.
∴△ADC≌△BOC,∠OCD=60°.
∴CD = OC,∠ADC =∠BOC=120°, AD= OB.
∴△OCD是等边三角形.
∴OC=OD=CD,∠COD=∠CDO=60°.
∵∠AOB=150°,∠BOC=120°,
∴∠AOC=90°.
∴∠AOD=30°,∠ADO=60°.
∴∠DAO=90°.
在Rt△ADO中,∠DAO=90°,
∴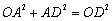 .
.
∴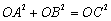 .
.
(2)①如图2,当α=β=120°时,OA+OB+OC有最小值.
作图如图2的实线部分.
如图2,将△AOC绕点C按顺时针方向旋转60°得△A’O’C,连接OO’.
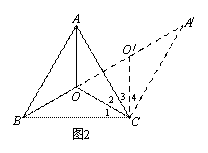 ∴△A’O’C≌△AOC,∠OCO’=∠ACA’=60°.
∴△A’O’C≌△AOC,∠OCO’=∠ACA’=60°.
∴O’C= OC, O’A’ = OA,A’C = BC,
∠A’O’C =∠AOC.
∴△OC O’是等边三角形.
∴OC= O’C = OO’,∠COO’=∠CO’O=60°.
∵∠AOB=∠BOC=120°,
∴∠AOC =∠A’O’C=120°.
∴∠BOO’=∠OO’A’=180°.
∴四点B,O,O’,A’共线.
∴OA+OB+OC= O’A’ +OB+OO’ =BA’ 时值最小.
②当等边△ABC的边长为1时,OA+OB+OC的最小值A’B=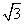 .
.


科目:初中数学 来源: 题型:
某地的一种绿色蔬菜,在市场上若直接销售,每吨利润为1000元,经粗加工后销售,每吨利润4000元,经精加工后销售,每吨利润7000元.当地一家公司现有这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨,如果对蔬菜进行精加工,每天可加工6吨,但每天两种方式不能同时进行.受季节等条件的限制,必须用15天时间将这批蔬菜全部销售或加工完毕.为此,公司研制了三种方案:
方案一:将蔬菜全部进行粗加工;
方案二:尽可能地对蔬菜进行精加工,没来得及加工的蔬菜,在市场上直接出售;
方案三:将一部分蔬菜进行精加工,其余蔬菜进行粗加工,并刚好15天完成.
如果你是公司经理,你会选择哪一种方案,说说理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
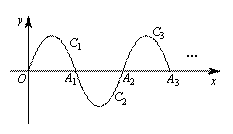
如右图,我们把抛物线y=-x(x-3)(0≤x≤3)记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2交x 轴于另一点A2;将C2绕点A2旋转180°得C3,交x 轴于另一点A3;……;如此进行下去,直至得C2016.①C1的对称轴方程是 ;②若点P(6047,m)在抛物线C2016上, 则m = .
查看答案和解析>>
科目:初中数学 来源: 题型:
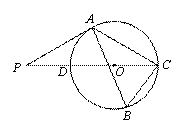
如右图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若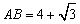 ,
,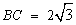 ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com