
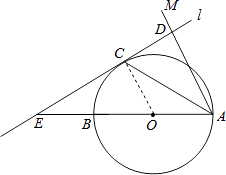
【题目】如图,AB为⊙O的直径,点C为⊙O上一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D. 
(1)试判断CD与⊙O的位置关系,并说明理由;
(2)若直线l与AB的延长线相交于点E,⊙O的半径为3,并且∠CAB=30°,求CE的长.
【答案】
(1)解:直线CD与⊙O相切.
理由如下:连接OC.
∵OA=OC,
∴∠BAC=∠OCA,
∵∠BAC=∠CAM,
∴∠OCA=∠CAM,
∴OC∥AM,
∵CD⊥AM,
∴OC⊥CD,
∵OC为半径,
∴直线CD与⊙O相切.
(2)解:∵OC=OA,
∴∠BAC=∠ACO,
∵∠CAB=30°,
∴∠COE=2∠CAB=60°,
∴在Rt△COE中,OC=3,CE=OCtan60°= ![]() .
.
【解析】(1)连接OC,根据OA=OC,推出∠BAC=∠OCA,求出∠OCA=∠CAM,推出OC∥AM,求出OC⊥CD,根据切线的判定推出即可;(2)根据OC=OA推出∠BAC=∠ACO,求出∠COE=2∠CAB=60°,在Rt△COE中,根据CE=OCtan60°求出即可.
【考点精析】解答此题的关键在于理解切线的判定定理的相关知识,掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线,以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


科目:初中数学 来源: 题型:
【题目】某校篮球队五名主力队员的身高分别是 173,180,181,176,178(单位:cm),则这五名运动员身高的中位数是( )
A. 181cm B. 180cm C. 178cm D. 176cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校课外小组为了解同学们对学校“阳光跑操”活动的喜欢程度,抽取部分学生进行调查.被调查的每个学生按A(非常喜欢)、B(比较喜欢)、C(一般)、D(不喜欢)四个等级对活动评价.图1和图2是该小组采集数据后绘制的两幅统计图.经确认扇形统计图是正确的,而条形统计图尚有一处错误且并不完整.请你根据统计图提供的信息,解答下列问题:

(1)此次调查的学生人数为___;
(2)条形统计图中存在错误的是___(填A. B.C中的一个),并在图中加以改正;
(3)在图2中补画条形统计图中不完整的部分;
(4)如果该校有600名学生,那么对此活动“非常喜欢”和“比较喜欢”的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 对角线互相平分的四边形是平行四边形
B. 对角线相等的四边形是矩形
C. 对角线互相垂直且平分的四边形是菱形
D. 邻边相等的矩形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
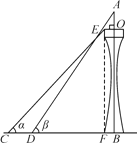
【题目】如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到1米,参考数据![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com