
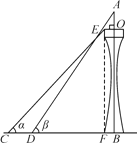
【题目】如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到1米,参考数据![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
科目:初中数学 来源: 题型:
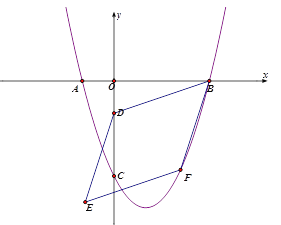
【题目】如图,在平面直角坐标系中,点A在x轴的负半轴上,B点坐标为(6,0),点C在y轴的负半轴上,且OB=OC,抛物线y=![]() x2+bx+c经过A、B、C三点.
x2+bx+c经过A、B、C三点.
(1)求此抛物线的函数关系式和点A的坐标;
(2)点D的坐标为(0,-2),F为该二次函数图像上的动点,连接BD、BF,以BD、BF为邻边作平行四边形BDEF,
①若点F为该二次函数在第四象限图像上的动点,设平行四边形BDEF的面积为S。求S的最大值。
②在点F的运动过程中,当点E落在一次函数y=x+7上时,求点F的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C为⊙O上一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D. 
(1)试判断CD与⊙O的位置关系,并说明理由;
(2)若直线l与AB的延长线相交于点E,⊙O的半径为3,并且∠CAB=30°,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC为直角三角形,∠ACB=900,AC=BC,点A、C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的抛物线过点B、D.
(1)求点A的坐标(用m表示);
(2)求抛物线的解析式;
(3)设点Q为抛物线上点P至点B之间的一动点,连结PQ并延长交BC于点E,连结BQ并延长交AC于点F,试证明:FC(AC+BC)为定值. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生对篮球、足球、排球、羽毛球、乒乓球这五种球类运动的喜爱情况,随机抽取一部分学生进行问卷调查,统计整理并绘制了以下两幅不完整的统计图:

请根据以上统计图提供的信息,解答下列问题:
(1)共抽取_____名学生进行问卷调查;
(2)补全条形统计图,求出扇形统计图中“篮球”所对应的圆心角的度数;
(3)该校共有2500名学生,请估计全校学生喜欢足球运动的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合运用
(1)某种花粉颗粒的半径为25μm,多少颗这样的花粉颗粒紧密排成一列的长度为1米?(1μm=10-6 m)
(2).已知(a+b)2=7, (a-b)2=3,求:①a2+b2; ②ab的值.
(3)已知10m=4,10n=5.求103m-2n+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场300名职工耕种51公顷土地,计划种植水稻,棉花和蔬菜,已知种植农作物每公顷所需的劳动力人数及投入的设备资金如下表:
农作物品种 | 每公顷需劳动力 | 每公顷需投入资金 |
水稻 | 4人 | 1万元 |
棉花 | 8人 | 1万元 |
蔬菜 | 5人 | 2万元 |
已知该农场计划在设备上投入67万元,应该怎样安排三种农作物的种植面积,才能使所有的职工都有工作,而且投入的资金正好够用?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com