
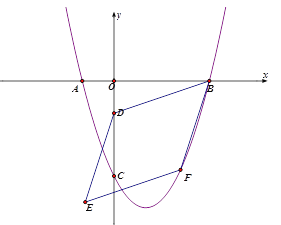
【题目】如图,在平面直角坐标系中,点A在x轴的负半轴上,B点坐标为(6,0),点C在y轴的负半轴上,且OB=OC,抛物线y=![]() x2+bx+c经过A、B、C三点.
x2+bx+c经过A、B、C三点.
(1)求此抛物线的函数关系式和点A的坐标;
(2)点D的坐标为(0,-2),F为该二次函数图像上的动点,连接BD、BF,以BD、BF为邻边作平行四边形BDEF,
①若点F为该二次函数在第四象限图像上的动点,设平行四边形BDEF的面积为S。求S的最大值。
②在点F的运动过程中,当点E落在一次函数y=x+7上时,求点F的坐标。
【答案】(1)y=![]() x2-x-6 ; A(-3,0);(2)①32;②F1(-3,0)F2(9,12)
x2-x-6 ; A(-3,0);(2)①32;②F1(-3,0)F2(9,12)
【解析】试题分析:(1)由OC=OB可得点C的坐标为(0,-6),再将点B、C的坐标代入抛物线y=![]() x2+bx+c中,即可得出抛物线的解析式,当y=0 时,求得x1=-3,x2=6,即点A的坐标为(-3,0);
x2+bx+c中,即可得出抛物线的解析式,当y=0 时,求得x1=-3,x2=6,即点A的坐标为(-3,0);
(2)①连接OF、DF,设点F的坐标为(t, ![]() 2-t-6),根据S四边形OBFD=S△OBD+S△BDF=SODF+S△OBF求得
2-t-6),根据S四边形OBFD=S△OBD+S△BDF=SODF+S△OBF求得![]() =-(t-2)2+16,由四边形BDEF是平行四边形得
=-(t-2)2+16,由四边形BDEF是平行四边形得![]() =
=![]() ,所以当
,所以当![]() 面积最大时,平行四边形BDEF的面积为S也有最大值.由
面积最大时,平行四边形BDEF的面积为S也有最大值.由![]() =-(t-2)2+16得:当t=2时,S△BDF有最大值=16,即平行四边形BDEF的面积S的最大值 为32.
=-(t-2)2+16得:当t=2时,S△BDF有最大值=16,即平行四边形BDEF的面积S的最大值 为32.
②设E点坐标为(m,m+7),由BD//EF,且BD=EF,则由D(0,-2)平移到B(6,0),则点E(m,m+7)平移到F(m+6,m+9),将F(m+6,m+9)代入y=![]() x2-x-6得m+9=
x2-x-6得m+9=![]() (m+6)2-(m+6)-6,即可求得m的值,即可求得F的坐标;
(m+6)2-(m+6)-6,即可求得m的值,即可求得F的坐标;
试题解析:
(1)∵OB=OC,B点坐标为(6,0),
∴点C坐标为(0,-6),
∵点B、C在抛物线y=![]() x2+bx+c上,
x2+bx+c上,
∴![]()
解得![]() ,
,
∴抛物线的解析式为:y=![]() x2-x-6
x2-x-6
当y=0时,即![]() x2-x-6 =0,解得x1=-3,x2=6,
x2-x-6 =0,解得x1=-3,x2=6,
所以A(-3
(2) ①连接OF、DF,如图所示:
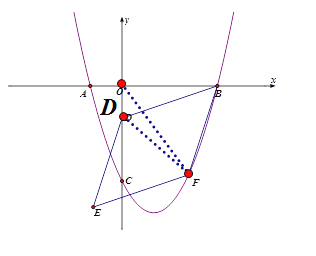
设点F的坐标为(t, ![]() 2-t-6),
2-t-6),
∴S△OBD+S△BDF =![]() ,
,
SODF+S△OBF=![]()
![]()
![]()
又∵S四边形OBFD=S△OBD+S△BDF=SODF+S△OBF
∴![]() =
=![]() ,即
,即![]() =
=![]() =-(t-2)2+16
=-(t-2)2+16
∵四边形BDEF是平行四边形,
∴![]() =
=![]() ,
,
∴当![]() 面积最大时,平行四边形BDEF的面积为S也有最大值.
面积最大时,平行四边形BDEF的面积为S也有最大值.
当t=2时,S△BDF有最大值=16,
∴平行四边形BDEF的面积S的最大值 为32.
当x=2时,S的最大值为32
②设E点坐标为(m,m+7),
∵BD//EF,且BD=EF,则由D(0,-2)平移到B(6,0),
∴点E(m,m+7)平移到F(m+6,m+9),
将F(m+6,m+9)代入y=![]() x2-x-6得m+9=
x2-x-6得m+9=![]() (m+6)2-(m+6)-6,
(m+6)2-(m+6)-6,
解得:m1=-9,m2=3,
所以F1(-3,0)或F2(9,12).


科目:初中数学 来源: 题型:
【题目】某校篮球队五名主力队员的身高分别是 173,180,181,176,178(单位:cm),则这五名运动员身高的中位数是( )
A. 181cm B. 180cm C. 178cm D. 176cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地教育行政部门计划今年暑假组织部分教师到外地进行学习,预订宾馆住宿时,有住宿条件一样的甲、乙两家宾馆供选择,其收费标准均为每人每天120元,并且各自推出不同的优惠方案.甲家是35人(含35人)以内的按标准收费,超过35人的,超出部分按九折收费;乙家是45人(含45人)以内的按标准收费,超过45人的,超出部分按八折收费.如果你是这个部门的负责人,你应选哪家宾馆更实惠些?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校课外小组为了解同学们对学校“阳光跑操”活动的喜欢程度,抽取部分学生进行调查.被调查的每个学生按A(非常喜欢)、B(比较喜欢)、C(一般)、D(不喜欢)四个等级对活动评价.图1和图2是该小组采集数据后绘制的两幅统计图.经确认扇形统计图是正确的,而条形统计图尚有一处错误且并不完整.请你根据统计图提供的信息,解答下列问题:

(1)此次调查的学生人数为___;
(2)条形统计图中存在错误的是___(填A. B.C中的一个),并在图中加以改正;
(3)在图2中补画条形统计图中不完整的部分;
(4)如果该校有600名学生,那么对此活动“非常喜欢”和“比较喜欢”的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
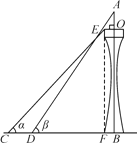
【题目】如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到1米,参考数据![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com