
【题目】如图,已知△ABC为直角三角形,∠ACB=900,AC=BC,点A、C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的抛物线过点B、D.
(1)求点A的坐标(用m表示);
(2)求抛物线的解析式;
(3)设点Q为抛物线上点P至点B之间的一动点,连结PQ并延长交BC于点E,连结BQ并延长交AC于点F,试证明:FC(AC+BC)为定值. 
【答案】(1)(![]() );(2)
);(2)![]() ;(3)见解析.
;(3)见解析.
【解析】试题分析:(1)AO=AC-OC=m-3,用线段的长度表示点A的坐标;(2)∵△ABC是等腰直角三角形,∴△AOD也是等腰直角三角形,∴OD=OA,∴D(0,m-3),又P(1,0)为抛物线顶点,可设顶点式,求解析式;(3)设Q(x,x2-2x+1),过Q点分别作x轴,y轴的垂线,运用相似比求出FC、EC的长,而AC=m,代入即可.
试题解析:(1) 由B(3,m)可知OC=3,BC=m,
又△ABC为等腰直角三角形,
∴AC=BC=m,OA=m-3,
∴点A的坐标是(3-m,0).
(2)∵∠ODA=∠OAD=45°
∴OD=OA=m-3,
则点D的坐标是(0,m-3).
又抛物线顶点为P(1,0),且过点B、D,
所以可设抛物线的解析式为:y=a(x-1)2,
得: ![]()
解得![]()
∴抛物线的解析式为y=x2-2x+1;
(3)证明:过点Q作QM⊥AC于点M,过点Q作QN⊥BC于点N,
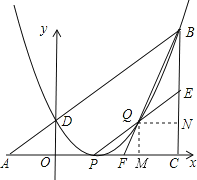
设点Q的坐标是(x,x2-2x+1),
则QM=CN=(x-1)2,MC=QN=3-x.
∵QM∥CE
∴△PQM∽△PEC
∴![]()
即![]() ,得EC=2(x-1)
,得EC=2(x-1)
∵QN∥FC
∴△BQN∽△BFC
∴![]() ,
,
即![]() ,得FC=
,得FC=![]()
又∵AC=4
∴FC(AC+EC)=![]() [4+2(x-1)]=
[4+2(x-1)]= ![]() (2x+2)=
(2x+2)=![]() ×2×(x+1)=8
×2×(x+1)=8
即FC(AC+EC)为定值8.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某校课外小组为了解同学们对学校“阳光跑操”活动的喜欢程度,抽取部分学生进行调查.被调查的每个学生按A(非常喜欢)、B(比较喜欢)、C(一般)、D(不喜欢)四个等级对活动评价.图1和图2是该小组采集数据后绘制的两幅统计图.经确认扇形统计图是正确的,而条形统计图尚有一处错误且并不完整.请你根据统计图提供的信息,解答下列问题:

(1)此次调查的学生人数为___;
(2)条形统计图中存在错误的是___(填A. B.C中的一个),并在图中加以改正;
(3)在图2中补画条形统计图中不完整的部分;
(4)如果该校有600名学生,那么对此活动“非常喜欢”和“比较喜欢”的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
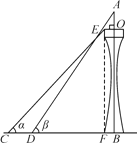
【题目】如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到1米,参考数据![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
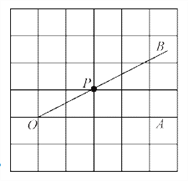
【题目】如图,在![]() 的正方形网格中,点P是
的正方形网格中,点P是![]() 的边OB上的一点.
的边OB上的一点.
(1)过点P画OB的垂线,交OA于点C;过点P画OA的垂线,垂足为H;
(2)线段PH的长度是点P到直线__________的距离;
(3)线段__________的长度是点C到直线OB的距离;
(4)线段PC、PH、OC这三条线段大小关系是__________(用“<”号连接).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com