
【题目】如图,直线y=﹣![]() x+
x+![]() 分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+
分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+![]() 经过A,B两点.
经过A,B两点.
(1)求A、B两点的坐标;
(2)求抛物线的解析式;
(3)点M是直线BC上方抛物线上的一点,过点M作MH⊥BC于点H,作MD∥y轴交BC于点D,求△DMH周长的最大值.
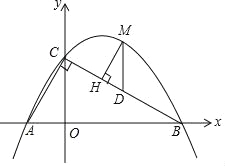
【答案】(1)(﹣1,0)(2)y=﹣![]() x2+
x2+![]() x+
x+![]() (3)
(3)![]()
【解析】
试题分析:(1)由直线解析式可求得B、C坐标,在Rt△BOC中由三角函数定义可求得∠OCB=60°,则在Rt△AOC中可得∠ACO=30°,利用三角函数的定义可求得OA,则可求得A点坐标;
(2)由A、B两点坐标,利用待定系数法可求得抛物线解析式;
(3)由平行线的性质可知∠MDH=∠BCO=60°,在Rt△DMH中利用三角函数的定义可得到DH、MH与DM的关系,可设出M点的坐标,则可表示出DM的长,从而可表示出△DMH的周长,利用二次函数的性质可求得其最大值.
试题解析: (1)∵直线y=﹣![]() x+
x+![]() 分别与x轴、y轴交于B、C两点,
分别与x轴、y轴交于B、C两点,
∴B(3,0),C(0,![]() ),
),
∴OB=3,OC=![]() ,
,
∴tan∠BCO=![]() =
=![]() ,
,
∴∠BCO=60°,
∵∠ACB=90°,
∴∠ACO=30°,
∴![]() =tan30°=
=tan30°=![]() ,即
,即![]() =
=![]() ,解得AO=1,
,解得AO=1,
∴A(﹣1,0);
(2)∵抛物线y=ax2+bx+![]() 经过A,B两点,
经过A,B两点,
∴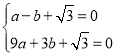 ,解得
,解得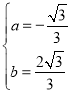 ,
,
∴抛物线解析式为y=﹣![]() x2+
x2+![]() x+
x+![]() ;
;
(3)∵MD∥y轴,MH⊥BC,
∴∠MDH=∠BCO=60°,则∠DMH=30°,
∴DH=![]() DM,MH=
DM,MH=![]() DM,
DM,
∴△DMH的周长=DM+DH+MH=DM+![]() DM+
DM+![]() DM=
DM=![]() DM,
DM,
∴当DM有最大值时,其周长有最大值,
∵点M是直线BC上方抛物线上的一点,
∴可设M(t,﹣![]() t2+
t2+![]() t+
t+![]() ),则D(t,﹣
),则D(t,﹣![]() t+
t+![]() ),
),
∴DM=﹣![]() t2+
t2+![]() t+
t+![]() ),则D(t,﹣
),则D(t,﹣![]() t+
t+![]() ),
),
∴DM=﹣![]() t2+
t2+![]() t+
t+![]() ﹣(﹣
﹣(﹣![]() t+
t+![]() )=﹣
)=﹣![]() t2+
t2+![]() t=﹣
t=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,
,
∴当t=![]() 时,DM有最大值,最大值为
时,DM有最大值,最大值为![]() ,
,
此时![]() DM=
DM=![]() ×
×![]() =
=![]() ,
,
即△DMH周长的最大值为![]() .
.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
【题目】下列命题中,假命题有( )
①两点之间线段最短;②到角的两边距离相等的点在角的平分线上;
③过一点有且只有一条直线与已知直线平行;④垂直于同一直线的两条直线平行;
⑤若⊙![]() 的弦
的弦![]() 交于点
交于点![]() ,则
,则![]() .
.
A.4个 B.3个 C. 2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,四边形ABCD是长方形,F是DA延长线上一点,CF交AB于点E,G是CF上一点,且AG=AC,∠ACG=2∠GAF.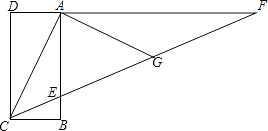
(1)若∠ACB=60°,求∠ECB的度数.
(2)若AF=12cm,AG=6.5cm,求△AEF中EF边上的高?
查看答案和解析>>
科目:初中数学 来源: 题型:
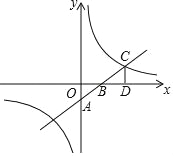
【题目】如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数y=![]() 的图象在第一象限的交点为C,CD⊥x轴,垂足为D,若OB=3,OD=6,△AOB的面积为3.
的图象在第一象限的交点为C,CD⊥x轴,垂足为D,若OB=3,OD=6,△AOB的面积为3.
(1)求一次函数与反比例函数的解析式;
(2)直接写出当x>0时,kx+b﹣![]() <0的解集.
<0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从某市5000名初一学生中,随机地抽取100名学生,测得他们的身高数据,得到一个样本,则这个样本数据的平均数、中位数、众数、方差四个统计量中,服装厂最感兴趣的是( )
A. 平均数 B. 中位数 C. 众数 D. 方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,张老师出示了问题:如图1,![]() 、
、![]() 是四边形
是四边形![]() 的对角线,若
的对角线,若![]()
![]() ,则线段
,则线段![]() ,
,![]() ,
,![]() 三者之间有何等量关系?
三者之间有何等量关系?
经过思考,小明展示了一种正确的思路:如图2,延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() ,证得
,证得![]() ,从而容易证明
,从而容易证明![]() 是等边三角形,故
是等边三角形,故![]() ,所以
,所以![]() .
.
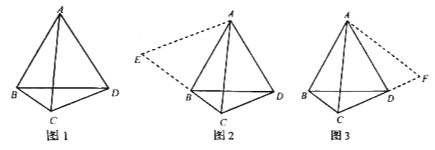
小亮展示了另一种正确的思路:如图3,将![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() ,使
,使![]() 与
与![]() 重合,从而容易证明
重合,从而容易证明![]() 是等比三角形,故
是等比三角形,故![]() ,所以
,所以![]() .
.
在此基础上,同学们作了进一步的研究:
(1)小颖提出:如图4,如果把“![]()
![]() ”改为“
”改为“![]()
![]() ”,其它条件不变,那么线段
”,其它条件不变,那么线段![]() ,
,![]() ,
,![]() 三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.
三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.
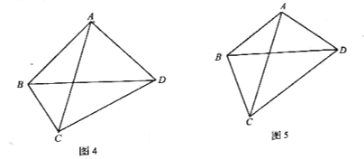
(2)小华提出:如图5,如果把“![]()
![]() ”改为“
”改为“![]()
![]() ”,其它条件不变,那么线段
”,其它条件不变,那么线段![]() ,
,![]() ,
,![]() 三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.
三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com