
【题目】已知,四边形ABCD是长方形,F是DA延长线上一点,CF交AB于点E,G是CF上一点,且AG=AC,∠ACG=2∠GAF.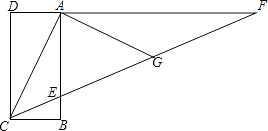
(1)若∠ACB=60°,求∠ECB的度数.
(2)若AF=12cm,AG=6.5cm,求△AEF中EF边上的高?
【答案】
(1)解:∵四边形ABCD是长方形,
∴DF∥BC,
∴∠AFC=∠ECB,
∵AC=AG,
∴∠ACG=∠AGC,
∵∠ACG=2∠GAF,∠AGC=∠GAF+∠F,
∴∠F=∠FAG,
∴∠ACG=2∠ECB,
∴∠ACB=∠ACG+∠ECB=3∠ECB=60°,
∴∠ECB=20°;
(2)解:设△AEF中EF边上的高为hcm,
∵∠F=∠FAG,
∴AG=GF,
∵∠BAF=90°,
∴∠EAG+∠GAF=90°,∠AEF+∠EFA=90°,
∴∠EAG=∠AEG,
∴EG=AG=GF,
∴EF=2AG=2×6.5=13(cm),
∴AE= ![]() =5(cm),
=5(cm),
∵△AEF的面积= ![]() AEAF=
AEAF= ![]() EFh,
EFh,
解得:h= ![]() cm,
cm,
即△AEF中EF边上的高为 ![]() cm.
cm.
【解析】(1)可利用平行线的性质,内错角相等可转化∠ECB=∠AFC,再由“AG=AC,∠ACG=2∠GAF”得出∠F=∠FAG,进而得出∠ACB=∠ACG+∠ECB=3∠ECB=60°,最后求出∠ECB的度数;(2)可证出EG=AG=GF,由勾股定理求出AE,再由面积法,即△AEF的面积= ![]() AEAF=
AEAF= ![]() EFh,求出h.
EFh,求出h.
【考点精析】掌握三角形的面积和等腰三角形的性质是解答本题的根本,需要知道三角形的面积=1/2×底×高;等腰三角形的两个底角相等(简称:等边对等角).


科目:初中数学 来源: 题型:
【题目】观察下列等式:21=2,22=4,23=8,24=16,25=32,26=64,…,根据这个规律,则21+22+23+24+…+22017的末位数字是( )
A.0
B.2
C.4
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+
x+![]() 分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+
分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+![]() 经过A,B两点.
经过A,B两点.
(1)求A、B两点的坐标;
(2)求抛物线的解析式;
(3)点M是直线BC上方抛物线上的一点,过点M作MH⊥BC于点H,作MD∥y轴交BC于点D,求△DMH周长的最大值.
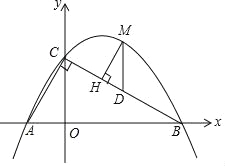
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把点M(-2,1)向右平移3个单位长度,再向下平移2个单位长度后得到点N,则点N的坐标为( )
A.(-4,4)B.(-5,3)C.(1,-1)D.(-5,-1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com