
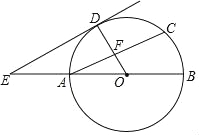
【题目】如图,![]() 为⊙
为⊙![]() 的直径,
的直径,![]() 为
为![]() 的中点,连接
的中点,连接![]() 交弦
交弦![]() 于点
于点![]() .过点
.过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)连接![]() ,若
,若![]() ,求四边形
,求四边形![]() 的面积.
的面积.
【答案】(1)证明见解析(2)8![]()
【解析】
试题分析:(1)欲证明DE是⊙O的切线,只要证明AC⊥OD,ED⊥OD即可.
(2)由△AFO≌△CFD(SAS),推出S△AFO=S△CFD,推出S四边形ACDE=S△ODE,求出△ODE的面积即可.
试题解析:(1)∵D为![]() 的中点,
的中点,
∴OD⊥AC,
∵AC∥DE,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)解:连接DC,
∵D为![]() 的中点,
的中点,
∴OD⊥AC,AF=CF,
∵AC∥DE,且OA=AE,
∴F为OD的中点,即OF=FD,
在△AFO和△CFD中,
∴△AFO≌△CFD(SAS),
∴S△AFO=S△CFD,
∴S四边形ACDE=S△ODE
在Rt△ODE中,OD=OA=AE=4,
∴OE=8,
∴DE=![]() =4
=4![]() ,
,
∴S四边形ACDE=S△ODE=![]() ×OD×DE=
×OD×DE=![]() ×4×4
×4×4![]() =8
=8![]() .
.


科目:初中数学 来源: 题型:
【题目】自从湖南与欧洲的“湘欧快线”开通后,我省与欧洲各国经贸往来日益频繁,某欧洲客商准备在湖南采购一批特色商品,经调查,用16000元采购![]() 型商品的件数是用7500元采购
型商品的件数是用7500元采购![]() 型商品的件数的2倍,一件
型商品的件数的2倍,一件![]() 型商品的进价比一件
型商品的进价比一件![]() 型商品的进价多10元.
型商品的进价多10元.
(1)求一件![]() 型商品的进价分别为多少元?
型商品的进价分别为多少元?
(2)若该欧洲客商购进![]() 型商品共250件进行试销,其中
型商品共250件进行试销,其中![]() 型商品的件数不大于
型商品的件数不大于![]() 型的件数,且不小于80件,已知
型的件数,且不小于80件,已知![]() 型商品的售价为240元/件,
型商品的售价为240元/件,![]() 型商品的售价为220元/件,且全部售出,设购进
型商品的售价为220元/件,且全部售出,设购进![]() 型商品
型商品![]() 件,求该客商销售这批商品的利润y与
件,求该客商销售这批商品的利润y与![]() 之间的函数关系式,并写出
之间的函数关系式,并写出![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,欧洲客商决定在试销活动中每售出一件![]() 型商品,就从一件
型商品,就从一件![]() 型商品的利润中捐献慈善资金
型商品的利润中捐献慈善资金![]() 元,求该客商售完所有商品并捐献资金后获得的最大收益.
元,求该客商售完所有商品并捐献资金后获得的最大收益.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,假命题有( )
①两点之间线段最短;②到角的两边距离相等的点在角的平分线上;
③过一点有且只有一条直线与已知直线平行;④垂直于同一直线的两条直线平行;
⑤若⊙![]() 的弦
的弦![]() 交于点
交于点![]() ,则
,则![]() .
.
A.4个 B.3个 C. 2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题探究发现
(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
填空:①∠AEB的度数为;②线段AD,BE之间的数量关系为 . 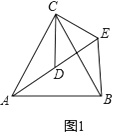
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.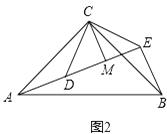
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 过点
过点![]() ,,与
,,与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线![]() 的函数表达式;
的函数表达式;
(2)若点![]() 在抛物线
在抛物线![]() 的对称轴上,求
的对称轴上,求![]() 的周长的最小值;
的周长的最小值;
(3)在抛物线![]() 的对称轴上是否存在点
的对称轴上是否存在点![]() ,使
,使![]() 是直角三角形?若存在,直接写出点
是直角三角形?若存在,直接写出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,四边形ABCD是长方形,F是DA延长线上一点,CF交AB于点E,G是CF上一点,且AG=AC,∠ACG=2∠GAF.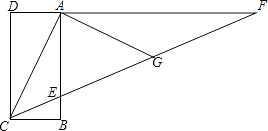
(1)若∠ACB=60°,求∠ECB的度数.
(2)若AF=12cm,AG=6.5cm,求△AEF中EF边上的高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,张老师出示了问题:如图1,![]() 、
、![]() 是四边形
是四边形![]() 的对角线,若
的对角线,若![]()
![]() ,则线段
,则线段![]() ,
,![]() ,
,![]() 三者之间有何等量关系?
三者之间有何等量关系?
经过思考,小明展示了一种正确的思路:如图2,延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() ,证得
,证得![]() ,从而容易证明
,从而容易证明![]() 是等边三角形,故
是等边三角形,故![]() ,所以
,所以![]() .
.
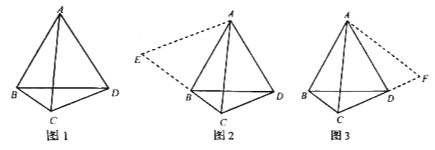
小亮展示了另一种正确的思路:如图3,将![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() ,使
,使![]() 与
与![]() 重合,从而容易证明
重合,从而容易证明![]() 是等比三角形,故
是等比三角形,故![]() ,所以
,所以![]() .
.
在此基础上,同学们作了进一步的研究:
(1)小颖提出:如图4,如果把“![]()
![]() ”改为“
”改为“![]()
![]() ”,其它条件不变,那么线段
”,其它条件不变,那么线段![]() ,
,![]() ,
,![]() 三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.
三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.
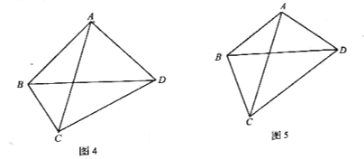
(2)小华提出:如图5,如果把“![]()
![]() ”改为“
”改为“![]()
![]() ”,其它条件不变,那么线段
”,其它条件不变,那么线段![]() ,
,![]() ,
,![]() 三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.
三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com