Question

【题目】综合题探究发现
（1）问题发现
如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE．
填空：①∠AEB的度数为；②线段AD，BE之间的数量关系为 ．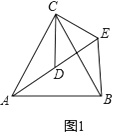

（2）拓展探究
如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A，D，E在同一直线上，CM为△DCE中DE边上的高，连接BE，请判断∠AEB的度数及线段CM，AE，BE之间的数量关系，并说明理由．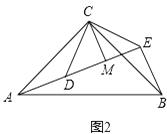

Answer 1

【答案】
（1）∠AEB=60°,AD=BE
（2）解：∠AEB=90°，AE=BE+2CM，

理由：如图2，

∵△ACB和△DCE均为等腰直角三角形，

∴CA=CB，CD=CE，∠ACB=∠DCE=90°，

∴∠ACD=∠BCE．

在△ACD和△BCE中，

，

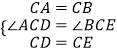∴△ACD≌△BCE（SAS），

∴AD=BE，∠ADC=∠BEC．

∵△DCE为等腰直角三角形，

∴∠CDE=∠CED=45°，

∵点A、D、E在同一直线上，

∴∠ADC=135°．

∴∠BEC=135°，

∴∠AEB=∠BEC﹣∠CED=90°．

∵CD=CE，CM⊥DE，

∴DM=ME．

∵∠DCE=90°，

∴DM=ME=CM，

∴AE=AD+DE=BE+2CM．

【解析】（1）利用等边三角形的性质可证出△ACD≌△BCE，进而得出∠ADC=∠BEC=120°；（2）借鉴（1）的方法，证△ACD≌△BCE，可得出AD=BE，∠ADC=∠BEC，进而得出AE=AD+DE=BE+2CM.