
分析 (1)根据“关联点”的定义结合点的坐标即可得出结论;
(2)根据点P在函数y=x-1的图象上,即可得出P(x,x-1)、Q(x,1),再根据点P、Q重合即可得出关于x的一元一次方程,解之即可得出结论;
(3)根据“关联点”的定义找出点N的坐标,分m≥n和m<n两种情况考虑,根据点N在函数y=x2的图象上,即可用含m的代数式表示出n,再根据两点间的距离公式即可找出MN的关系式,利用一次(二次)函数的性质即可求出线段MN的最大值.
解答 解:(1)∵|2-2|=0,
∴点(2,2)的“关联点”的坐标为(2,0).
(2)∵点P在函数y=x-1的图象上,
∴P(x,x-1),则点Q的坐标为(x,1),
∵点Q与点P重合,
∴x-1=1,解得:x=2,
∴点P的坐标为(2,1).
(3)∵点M(m,n),
∴点N(m,|m-n|).
∵点N在函数y=x2的图象上,
∴|m-n|=m2.
(i)当m≥n时,m-n=m2,
∴n=-m2+m,
∴M(m,-m2+m),N(m,m2).
∵0≤m≤2,
∴MN=|yM-yN|=|-m2+m-m2|=m|2m-1|.
①当0≤m≤$\frac{1}{2}$时,MN=-2m2+m=-2$(x-\frac{1}{4})^{2}$+$\frac{1}{8}$,
∴当m=$\frac{1}{4}$时,MN取最大值,最大值为$\frac{1}{8}$.
②当$\frac{1}{2}$<m≤2时,MN=2m2-m=2$(x-\frac{1}{4})^{2}$+$\frac{1}{8}$,
当m=2时,MN取最大值,最大值为6.
(ii)当m<n时,n-m=m2,
∴n=m2+m,
∴M(m,m2+m),N(m,m2).
∵0≤m≤2,
∴MN=|yM-yN|=|m2+m-m2|=m,
当m=2时,MN取最大值2.
点评 本题考查了二次函数的性质、一次函数的性质、一次函数图象上点的坐标特征、二次函数图象上点的坐标特征以及解一元一次方程,解题的关键是:(1)根据“关联点”的定义找出点的关联点;(2)根据点P、Q重合找出关于x的一元一次方程;(3)用含m的代数式表示出n.


 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 运输工具 | 途中平均速度(千米/时) | 运费(元/千米) | 装卸费用(元) |
| 火车 | 100 | 15 | 2000 |
| 汽车 | 80 | 20 | 900 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
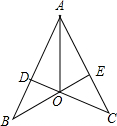 如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE与CD相交于点O,且AD=AE,有以下结论:①∠B=∠C,②△ADO≌△AEO;③△BOD≌△COE;④图中有四组三角形全等,其中正确的结论有( )
如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE与CD相交于点O,且AD=AE,有以下结论:①∠B=∠C,②△ADO≌△AEO;③△BOD≌△COE;④图中有四组三角形全等,其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 单项式$\frac{1}{2}$xy的系数是$\frac{1}{2}$,次数是1 | |
| B. | 单项式-$\frac{1}{3}$πa2b3的系数是-$\frac{1}{3}$,次数是6 | |
| C. | 单项式x2的系数是1,次数是2 | |
| D. | 多项式2x3-3x2y2+x-1叫三次四项式 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com