
如果二次函数的二次项系数为l,则此二次函数可表示为y=x2+px+q,我们称[p,q]为此函数的特征数,如函数y=x2+2x+3的特征数是[2,3].
(1)若一个函数的特征数为[﹣2,1],求此函数图象的顶点坐标.
(2)探究下列问题:
①若一个函数的特征数为[4,﹣1],将此函数的图象先向右平移1个单位,再向上平移1个单位,求得到的图象对应的函数的特征数.
②若一个函数的特征数为[2,3],问此函数的图象经过怎样的平移,才能使得到的图象对应的函数的特征数为[3,4]?
(1)(1,0);(2)①[2,﹣3];②原函数的图象向左平移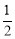 个单位,再向下平移
个单位,再向下平移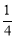 个单位得到.
个单位得到.
【解析】
试题分析:(1)根据题意得出函数解析式,进而得出顶点坐标即可.
(2)①首先得出函数解析式,进而利用函数平移规律得出答案;
②分别求出两函数解析式,进而得出平移规律.
试题解析:【解析】
(1)由题意可得出:y=x2﹣2x+1=(x﹣1)2,
∴此函数图象的顶点坐标为:(1,0).
(2)①由题意可得出:y=x2+4x﹣1=(x+2)2﹣5,
∴将此函数的图象先向右平移1个单位,再向上平移1个单位后得到:
y=(x+1)2﹣4=x2+2x﹣3.
∴图象对应的函数的特征数为:[2,﹣3].
②∵一个函数的特征数为[2,3],
∴函数解析式为:y=x2+2x+3=(x+1)2+2,
∵一个函数的特征数为[3,4],
∴函数解析式为: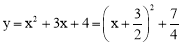 .
.
∴原函数的图象向左平移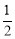 个单位,再向下平移
个单位,再向下平移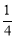 个单位得到.
个单位得到.
考点:1.新定义和阅读理解型问题;2.二次函数图象与平移变换;3.二次函数的性质


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源:2014年初中毕业升学考试(广东深圳卷)数学(解析版) 题型:解答题
某“爱心义卖”活动中,购进甲、乙两种文具,甲每个进货价高于乙进货价10元,90元买乙的数量与150元买甲的数量相同.
(1)求甲、乙进货价;
(2)甲、乙共100件,将进价提高20%进行销售,进货价少于2080元,销售额要大于2460元,求有几种方案?
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西钦州卷)数学(解析版) 题型:解答题
甲口袋中装有3个相同的小球,它们分别写有数值﹣1,1,5;乙口袋中装有3个相同的小球,它们分别写有数值﹣4,2,3.现从甲口袋中随机取一球,记它上面的数值为x,再从乙口袋中随机取一球,记它上面的数值为y.设点A的坐标为(x,y),请用树形图或列表法,求点A落在第一象限的概率.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江嘉兴卷)数学(解析版) 题型:解答题
类比梯形的定义,我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
(1)已知:如图1,四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=70°,∠B=80°.求∠C,∠D的度数.
(2)在探究“等对角四边形”性质时:
①小红画了一个“等对角四边形”ABCD(如图2),其中∠ABC=∠ADC,AB=AD,此时她发现CB=CD成立.请你证明此结论;
②由此小红猜想:“对于任意‘等对角四边形’,当一组邻边相等时,另一组邻边也相等”.你认为她的猜想正确吗?若正确,请证明;若不正确,请举出反例.
(3)已知:在“等对角四边形"ABCD中,∠DAB=60°,∠ABC=90°,AB=5,AD=4.求对角线AC的长.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(海南卷)数学(解析版) 题型:选择题
据报道,我省西环高铁预计2015年底建成通车,计划总投资27100 000 000元,数据27 100 000 000用科学记数法表示为( )
A.271×108 B.2.71×109 C.2.71×1010 D.2.71×1011
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江绍兴卷)数学(解析版) 题型:选择题
如图,汽车在东西向的公路l上行驶,途中A,B,C,D四个十字路口都有红绿灯.AB之间的距离为800米,BC为1000米,CD为1400米,且l上各路口的红绿灯设置为:同时亮红灯或同时亮绿灯,每次红(绿)灯亮的时间相同,红灯亮的时间与绿灯亮的时间也相同.若绿灯刚亮时,甲汽车从A路口以每小时30千米的速度沿l向东行驶,同时乙汽车从D路口以相同的速度沿l向西行驶,这两辆汽车通过四个路口时都没有遇到红灯,则每次绿灯亮的时间可能设置为( )

A.50秒 B.45秒 C.40秒 D.35秒
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(海南卷)数学(解析版) 题型:解答题
如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1464米到B点处测得正前方C点处的俯角为45°.求海底C点处距离海面DF的深度(结果精确到个位,参考数据: ≈1.414,
≈1.414, ≈1.732,
≈1.732, ≈2.236).
≈2.236).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com