
类比梯形的定义,我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
(1)已知:如图1,四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=70°,∠B=80°.求∠C,∠D的度数.
(2)在探究“等对角四边形”性质时:
①小红画了一个“等对角四边形”ABCD(如图2),其中∠ABC=∠ADC,AB=AD,此时她发现CB=CD成立.请你证明此结论;
②由此小红猜想:“对于任意‘等对角四边形’,当一组邻边相等时,另一组邻边也相等”.你认为她的猜想正确吗?若正确,请证明;若不正确,请举出反例.
(3)已知:在“等对角四边形"ABCD中,∠DAB=60°,∠ABC=90°,AB=5,AD=4.求对角线AC的长.

(1)130°,80°;(2)①证明见解析;②不正确,反例见解析;(3)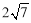 或
或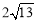 .
.
【解析】
试题分析:(1)根据定义和四边形内角和定理求解即可.
(2)①连接BD,根据定义以及等腰三角形的判定和性质求证即可.
②当相等角的两边相等时,结论不正确.
(3)分∠ADC=∠ABC=90°和∠BCD=∠DAB=60°两种情况讨论即可.
试题解析:(1)∵等对角四边形ABCD中,∠A≠∠C,∠B=80°,∴∠D=∠B=80°.
∵∠A=70°,∴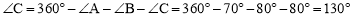 .
.
(2)①如图,连接BD,
∵AB=AD,∴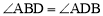 .
.
∵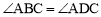 ,∴
,∴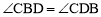 .
.
∴CB=CD.
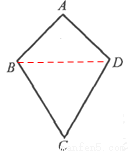
②不正确,反例如图,∠A=∠C=90°,AB=AD,但CB≠CD.
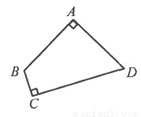
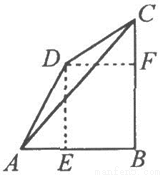
(3)①如图,当∠ADC=∠ABC=90°时,延长AD,BC交于点F,
∵∠ABC=90°,∠DAB=60°,AB=5,∴AE=10.
∴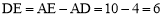 .
.
∵∠EDC=90°,∠E=30°,∴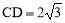 .
.
∴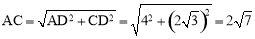 .
.
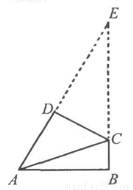
②如图,当∠BCD=∠DAB=60°时,过D点作DE⊥AB于点E,DF⊥BC于点F,
∵DE⊥AB,∠DAB=60°,AD=4,∴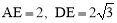 .
.
∴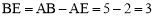 .
.
∵四边形BFDE是矩形,∵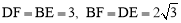 .
.
∵∠BCD=60°,∴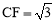 .∴
.∴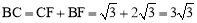 .
.
∴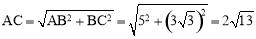
考点:1.新定义和阅读理解型问题;2.四边形内角和定理;3.等腰三角形的判定和性质;4.勾股定理;5.含30度角直角性质;6.分类思想和反证法的应用.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源:2014年初中毕业升学考试(广西钦州卷)数学(解析版) 题型:填空题
如图,△A′B′C′是△ABC经过某种变换后得到的图形,如果△ABC中有一点P的坐标为(a,2),那么变换后它的对应点Q的坐标为 .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江绍兴卷)数学(解析版) 题型:解答题
如果二次函数的二次项系数为l,则此二次函数可表示为y=x2+px+q,我们称[p,q]为此函数的特征数,如函数y=x2+2x+3的特征数是[2,3].
(1)若一个函数的特征数为[﹣2,1],求此函数图象的顶点坐标.
(2)探究下列问题:
①若一个函数的特征数为[4,﹣1],将此函数的图象先向右平移1个单位,再向上平移1个单位,求得到的图象对应的函数的特征数.
②若一个函数的特征数为[2,3],问此函数的图象经过怎样的平移,才能使得到的图象对应的函数的特征数为[3,4]?
查看答案和解析>>
科目:初中数学 来源:2014年沪教版初中数学七年级上册第九章9.3整式的乘法练习卷(解析版) 题型:选择题
a12不能写成( )
A.(a3)4 B.(a6)2 C.(a2)10 D.a2•a10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com