
 ЪЧЮоРэЪ§ЃЌЖјЮоРэЪ§ЪЧЮоЯоВЛбЛЗаЁЪ§ЃЌвђДЫ
ЪЧЮоРэЪ§ЃЌЖјЮоРэЪ§ЪЧЮоЯоВЛбЛЗаЁЪ§ЃЌвђДЫ ЕФаЁЪ§ВПЗжЮвУЧВЛПЩФмШЋВПЕиаДГіРДЃЌгкЪЧаЁУїгУ
ЕФаЁЪ§ВПЗжЮвУЧВЛПЩФмШЋВПЕиаДГіРДЃЌгкЪЧаЁУїгУ РДБэЪО
РДБэЪО ЕФаЁЪ§ВПЗжЃЌФуЭЌвтаЁУїЕФБэЪОЗНЗЈТ№ЃП
ЕФаЁЪ§ВПЗжЃЌФуЭЌвтаЁУїЕФБэЪОЗНЗЈТ№ЃП ЕФећЪ§ВПЗжЪЧ1ЃЌНЋетИіЪ§МѕШЅЦфећЪ§ВПЗжЃЌВюОЭЪЧаЁЪ§ВПЗжЃЎ
ЕФећЪ§ВПЗжЪЧ1ЃЌНЋетИіЪ§МѕШЅЦфећЪ§ВПЗжЃЌВюОЭЪЧаЁЪ§ВПЗжЃЎ ЃЌМД
ЃЌМД ЃЌ
ЃЌ ЕФећЪ§ВПЗжЮЊ2ЃЌаЁЪ§ВПЗжЮЊ
ЕФећЪ§ВПЗжЮЊ2ЃЌаЁЪ§ВПЗжЮЊ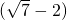 ЃЎ
ЃЎ ЕФаЁЪ§ВПЗжЮЊaЃЌ
ЕФаЁЪ§ВПЗжЮЊaЃЌ ЕФећЪ§ВПЗжЮЊbЃЌЧѓ
ЕФећЪ§ВПЗжЮЊbЃЌЧѓ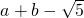 ЕФжЕЃЛ
ЕФжЕЃЛ ЃЌЦфжаxЪЧећЪ§ЃЌЧв0ЃМyЃМ1ЃЌЧѓx-yЕФЯрЗДЪ§ЃЎ
ЃЌЦфжаxЪЧећЪ§ЃЌЧв0ЃМyЃМ1ЃЌЧѓx-yЕФЯрЗДЪ§ЃЎ ЃМ3ЃЌ
ЃМ3ЃЌ ЕФаЁЪ§ВПЗжa=
ЕФаЁЪ§ВПЗжa= -2 Ђй
-2 Ђй ЃМ4ЃЌ
ЃМ4ЃЌ ЕФећЪ§ВПЗжЮЊb=3 Ђк
ЕФећЪ§ВПЗжЮЊb=3 Ђк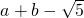 ЃЌЕУ
ЃЌЕУ -2+3
-2+3 =1ЃЌМД
=1ЃЌМД ЃЎ
ЃЎ ЃМ3ЃЌ
ЃМ3ЃЌ ЕФећЪ§ВПЗжЪЧ1ЁЂаЁЪ§ВПЗжЪЧ
ЕФећЪ§ВПЗжЪЧ1ЁЂаЁЪ§ВПЗжЪЧ ЃЌ
ЃЌ =10+1+ЃЈ
=10+1+ЃЈ =11+ЃЈ
=11+ЃЈ ЃЉЃЌ
ЃЉЃЌ ЃЌ
ЃЌ ЃЉ=x+yЃЌ
ЃЉ=x+yЃЌ ЃЛ
ЃЛ ЃЉ=12-
ЃЉ=12- ЃЌ
ЃЌ ЃЎ
ЃЎ ЁЂ
ЁЂ ЕФНќЫЦжЕЃЌШЛКѓХаЖЯ
ЕФНќЫЦжЕЃЌШЛКѓХаЖЯ ЕФаЁЪ§ВПЗжaЃЌ
ЕФаЁЪ§ВПЗжaЃЌ ЕФећЪ§ВПЗжbЃЌзюКѓНЋaЁЂbЕФжЕДњШы
ЕФећЪ§ВПЗжbЃЌзюКѓНЋaЁЂbЕФжЕДњШы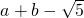 ВЂЧѓжЕЃЛ
ВЂЧѓжЕЃЛ ЕФНќЫЦжЕЃЌШЛКѓХаЖЯ
ЕФНќЫЦжЕЃЌШЛКѓХаЖЯ ЕФећЪ§ВПЗжВЂЧѓЕУxЁЂyЕФжЕЃЌзюКѓЧѓx-yЕФЯрЗДЪ§ЃЎ
ЕФећЪ§ВПЗжВЂЧѓЕУxЁЂyЕФжЕЃЌзюКѓЧѓx-yЕФЯрЗДЪ§ЃЎ


| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКдФЖСРэНт
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 4 |
| 7 |
| 9 |
| 7 |
| 7 |
| 7 |
| 13 |
| 3 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКдФЖСРэНт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКдФЖСРэНт
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 4 |
| 7 |
| 9 |
| 7 |
| 7 |
| 7 |
| 5 |
| 13 |
| 5 |
| 3 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКдФЖСРэНт
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 11 |
| 11 |
| 11 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКдФЖСРэНт
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 5 |
| 5 |
| 5 |
| 2 |
| 2 |
| 2 |
| 3 |
| 3 |
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com