
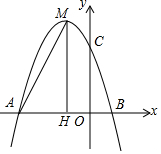
 如图,在平面直角坐标系中,抛物线与x轴分别交A(-3,0),B(1,0),交y轴于点C(0,3),过顶点M作MH⊥x轴于点H.
如图,在平面直角坐标系中,抛物线与x轴分别交A(-3,0),B(1,0),交y轴于点C(0,3),过顶点M作MH⊥x轴于点H.分析 (1)由题意可以假设抛物线的解析式为y=a(x+3)(x-1),把(0,3)代入求出a即可.
(2)如图1中,如图1,假设在y轴上存在满足条件的点D,过点M作ME⊥y轴于点E.设D(0,c),由△MED∽△DOA,得$\frac{ME}{DO}$=$\frac{DE}{OA}$列出方程即可解决问题.
(3)分两种情形)①当点P在对称轴右侧时,如图2中,只能是△PCQ∽△CAH,得∠QMP=∠MAH,延长CP交x轴于M,②当点P在对称轴左侧时,只能是△PMQ∽△ACH,得到∠PMQ=∠ACH,过A作AM的垂线交MP的延长线于F,作FN⊥x轴于N.分别求解即可.
(4)观察图象求出AN的最大值以及最小值即可解决问题.
解答 解:(1)由题意可以假设抛物线的解析式为y=a(x+3)(x-1),
把(0,3)代入得到,3=-3a,
∴a=-1,
∴抛物线的解析式为y=-x2-2x+3.
(2)如图1中,如图1,假设在y轴上存在满足条件的点D,过点M作ME⊥y轴于点E.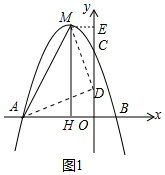
由∠MDA=90°得∠ADO+∠MDE=90°.
又∵∠DAO+∠ADO=90°,
∴∠EDM=∠DAO,
又∵∠MED=∠DOA=90°,
∴△MED∽△DOA,
∴$\frac{ME}{DO}$=$\frac{DE}{OA}$.
设D(0,c),
则 $\frac{1}{c}$=$\frac{4-c}{3}$.
变形,得c2-4c+3=0,
解得c1=3,c2=1.
综合上述:在y轴上存在点D(0,3)或(0,1),使△AMD是以AM为斜边的直角三角形.
(3)①当点P在对称轴右侧时,如图2中,只能是△PCQ∽△CAH,得∠QMP=∠MAH,延长CP交x轴于M,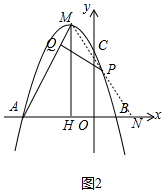
∴AN=NM,设N(m,0),则有(m+3)2=42+(m+1)2,
∴m=2,即N(2,0),设直线NM的解析式为y=kx+b,则有$\left\{\begin{array}{l}{-k+b=4}\\{2k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{4}{3}}\\{b=\frac{8}{3}}\end{array}\right.$,
∴直线MN的解析式为y=$\frac{4}{3}$x+$\frac{8}{3}$,
由$\left\{\begin{array}{l}{y=\frac{4}{3}x+\frac{8}{3}}\\{y=-{x}^{2}-2x+3}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{1}{3}}\\{y=\frac{20}{9}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=4}\end{array}\right.$(舍弃),
∴P($\frac{1}{3}$,$\frac{20}{9}$).
②当点P在对称轴左侧时,只能是△PMQ∽△ACH,得到∠PMQ=∠ACH,过A作AM的垂线交MP的延长线于F,作FN⊥x轴于N.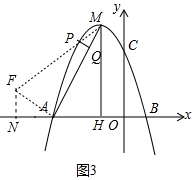
由△MFA∽△CAH得$\frac{MA}{MH}$=$\frac{AF}{AH}$=2,
由△FNA∽△CAH得$\frac{FN}{AH}$=$\frac{NA}{MH}$=$\frac{AF}{AM}$=$\frac{1}{2}$,
∴AN=2,FN=1,MH=4,OH=1,
∴F(-5,1),∵C(-1,4),
∴直线CF的解析式为y=$\frac{3}{4}$x+$\frac{19}{4}$,
由$\left\{\begin{array}{l}{y=\frac{3}{4}x+\frac{19}{4}}\\{y=-{x}^{2}-2x+3}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{7}{4}}\\{y=\frac{55}{16}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=4}\end{array}\right.$(舍弃),
∴P($\frac{7}{4}$,$\frac{55}{16}$),
综上所述,点P坐标为P($\frac{1}{3}$,$\frac{20}{9}$)或($\frac{7}{4}$,$\frac{55}{16}$).
(4)如图4中,作EQ⊥AB于Q,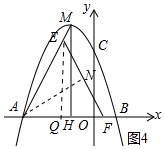
观察图象可知,当AE=AF时,AN的值最大,
由△AEQ∽△AMH,得到$\frac{EQ}{AQ}$=$\frac{MH}{AH}$=$\frac{1}{2}$,设AQ=x,则EQ=2x,AE=AF=$\sqrt{5}$x,
在Rt△EQF中,∵∠EQF=90°,EF=4,QF=$\sqrt{5}$x-x,
∴(2x)2+($\sqrt{5}$x-x)2=16,
∴x2=$\frac{8}{5-\sqrt{5}}$,
在Rt△ANF中,AN=$\sqrt{A{F}^{2}-F{N}^{2}}$=$\sqrt{5×\frac{8}{5-\sqrt{5}}-4}$=$\sqrt{5}$+1,
∴AN的最大值为$\sqrt{5}$+1,
当点E与A重合时,AN的值最小为2,
∴EF的中点N与点A距离的取值范围是:2≤AN≤$\sqrt{5}$+1.
故答案为2≤AN≤$\sqrt{5}$+1.
点评 此题主要考查了二次函数的综合应用以及相似三角形的应用,二次函数的综合应用是初中阶段的重点题型,特别注意利用数形结合是这部分考查的重点,学会取特殊位置解决最值问题,题目比较难,属于中考压轴题.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
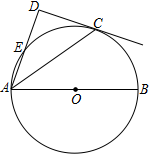 如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E
如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com