
“抢红包”是2015年春节十分火爆的一项网络活动,某企业有4000名职工,从中随机抽取350人,按年龄分布和对“抢红包”所持态度情况进行了调查,并将调查结果绘成了条形统计图和扇形统计图.


(1)这次调查中,如果职工年龄的中位数是整数,那么这个中位数所在的年龄段是哪一段?
(2)如果把对“抢红包”所持态度中的“经常(抢红包)”和“偶尔(抢红包)”统称为“参与抢红包”,那么这次接受调查的职工中“参与抢红包”的人数是多少?
(3)请估计该企业“从不(抢红包)”的人数是多少?
【考点】条形统计图;用样本估计总体;扇形统计图;中位数.
【分析】(1)根据中位数的概念和抽查的人数确定中位数所在的范围;
(2)求出“参与抢红包”的人数所占的百分比,求出人数;
(3)求出从不(抢红包)”的人数所占是百分比,求出该企业“从不(抢红包)”的人数.
【解答】解:(1)∵抽取350人,∴中位数是175和176的平均数,
∴中位数所在的年龄段是25﹣35;
(2)这次接受调查的职工中“参与抢红包”的人数是:350×(40%+22%)=217人;
(3)估计该企业“从不(抢红包)”的人数是:4000×(1﹣40%﹣22%)=1520人.
【点评】本题考查的是条形图、扇形图、中位数的概念和用样本估计总体的知识,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.


科目:初中数学 来源: 题型:
如图,在△ABC中,AC>AB,AD是角平分线,AE是中线,BF⊥AD于点G,交AE于点F,交AC于点M,EG的延长线交AB于点H
(1) 求证:AH=BH
(2) 若∠BAC=60°,求 的值
的值


查看答案和解析>>
科目:初中数学 来源: 题型:
如图,□ABCD的顶点坐标分别为A(1,4)、B(1,1)、C(5,2),则点D的坐标为( )
A.(5,5) B.(5,6) C.(6,6) D.(5,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
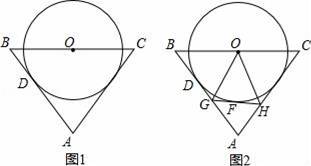
如图1,△ABC中,AB=AC,点O是BC的中点,以O为圆心的⊙O与AB边相切于点D.
(1)判断AC边与⊙O的位置关系,说明理由;
(2)如图2,若AB=5,BC=6,点F为⊙O上一动点,过点F作⊙O的切线分别交AD边、AC边于点G、H,连结OG、OH.
①设∠BAC=α,则∠GOH= (用含α的代数式表示);
②若△OGH是以GH为腰的等腰三角形,求BG的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com