
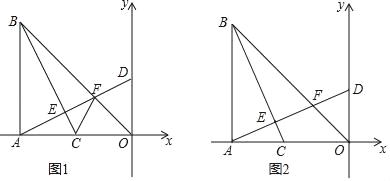
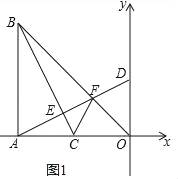
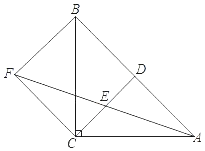
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABOжаЃЌЁЯBAOЃН90ЁуЃЌAOЃНABЃЌBOЃН8![]() ЃЌЕуAЕФзјБъЃЈЉ8ЃЌ0ЃЉЃЌЕуCдкЯпЖЮAOЩЯвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШгЩAЯђOдЫЖЏЃЌдЫЖЏЪБМфЮЊtУыЃЌСЌНгBCЃЌЙ§ЕуAзїADЁЭBCЃЌДЙзуЮЊЕуEЃЌЗжБ№НЛBOгкЕуFЃЌНЛyжсгкЕу DЃЎ
ЃЌЕуAЕФзјБъЃЈЉ8ЃЌ0ЃЉЃЌЕуCдкЯпЖЮAOЩЯвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШгЩAЯђOдЫЖЏЃЌдЫЖЏЪБМфЮЊtУыЃЌСЌНгBCЃЌЙ§ЕуAзїADЁЭBCЃЌДЙзуЮЊЕуEЃЌЗжБ№НЛBOгкЕуFЃЌНЛyжсгкЕу DЃЎ
ЃЈ1ЃЉгУtБэЪОЕуDЕФзјБъЁЁ ЁЁЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌСЌНгCFЃЌЕБtЃН2ЪБЃЌЧѓжЄЃКЁЯFCOЃНЁЯBCAЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЕБBCЦНЗжЁЯABOЪБЃЌЧѓtЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉЃЈ0ЃЌ2tЃЉЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉt=4ЃЈ![]() Љ1ЃЉ
Љ1ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩвбжЊЬѕМўПЩжЄУїЁїABCЁеЁїOADЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪМДПЩЧѓГіЕуDЕФзјБъЃЛ
ЃЈ2ЃЉгЩЃЈ1ЃЉЕФНсТлПЩжЄУїЁїFODЁеЁїFOCЃЌДгЖјЁЯFCOЃНЁЯFDOЃЌдйИљОнЃЈ1ЃЉжаЁїABCЁеЁїOADЃЌПЩЕУЁЯACBЃНЁЯADOЃЌНјЖјЁЯFCOЃНЁЯACBЕУжЄЃЛ
ЃЈ3ЃЉдкABЩЯШЁвЛЕуKЃЌЪЙЕУAKЃНACЃЌСЌНгCKЃЎЩшAKЃНACЃНmЃЌдђCKЃН![]() mЃЌИљОнНЧЦНЗжЯпЕФаджЪКЭШ§НЧаЮЭтНЧКЭЖЈРэПЩЕУKBЃНKCЃН
mЃЌИљОнНЧЦНЗжЯпЕФаджЪКЭШ§НЧаЮЭтНЧКЭЖЈРэПЩЕУKBЃНKCЃН![]() mЃЌДгЖјЧѓЕУmЕФжЕЃЌНјЖјtЕФжЕвВПЩЧѓГі.
mЃЌДгЖјЧѓЕУmЕФжЕЃЌНјЖјtЕФжЕвВПЩЧѓГі.
НтЃКЃЈ1ЃЉЁпADЁЭBCЃЌ
ЁрЁЯAEBЃН90ЁуЃНЁЯBACЃНЁЯAODЃЌ
ЁрЁЯABC+ЁЯBAEЃН90ЁуЃЌЁЯBAE+ЁЯOADЃН90ЁуЃЌ
ЁрЁЯABCЃНЁЯOADЃЌ
ЁпABЃНOAЃЌ
ЁрЁїABCЁеЁїOADЃЈASAЃЉЃЌ
ЁрODЃНACЃН2tЃЌ
ЁрDЃЈ0ЃЌ2tЃЉЃЎ
ЙЪД№АИЮЊЃЈ0ЃЌ2tЃЉЃЛ
ЃЈ2ЃЉШчЭМ1жаЃЌ
ЁпABЃНAOЃЌЁЯBAOЃН90ЁуЃЌOBЃН![]() ЃЌ
ЃЌ
ЁрABЃНAOЃН8ЃЌ
ЁпtЃН2ЃЌ
ЁрACЃНODЃН4ЃЌ
ЁрOCЃНODЃН4ЃЌ
ЁпOFЃНOFЃЌЁЯFODЃНЁЯFOCЃЌ
ЁрЁїFODЁеЁїFOCЃЈSASЃЉЃЌ
ЁрЁЯFCOЃНЁЯFDOЃЌ
ЁпЁїABCЁеЁїOADЃЌ
ЁрЁЯACBЃНЁЯADOЃЌ
ЁрЁЯFCOЃНЁЯACBЃЛ
ЃЈ3ЃЉШчЭМ2жаЃЌдкABЩЯШЁвЛЕуKЃЌЪЙЕУAKЃНACЃЌСЌНгCKЃЎЩшAKЃНACЃНmЃЌдђCKЃН![]() mЃЎ
mЃЎ
ЁпCBЦНЗжЁЯABOЃЌ
ЁрЁЯABCЃН22.5ЁуЃЌ
ЁпЁЯAKCЃН45ЁуЃНЁЯABC+ЁЯKCBЃЌ
ЁрЁЯKBCЃНЁЯKCBЃН22.5ЁуЃЌ
ЁрKBЃНKCЃН![]() mЃЌ
mЃЌ
Ёрm+![]() mЃН8ЃЌ
mЃН8ЃЌ
ЁрmЃН8ЃЈ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрtЃН![]() ЃН4ЃЈ
ЃН4ЃЈ![]() Љ1ЃЉЃЎ
Љ1ЃЉЃЎ


 ЧсЧЩЖсЙкжмВтдТПМжБЭЈжаПМЯЕСаД№АИ
ЧсЧЩЖсЙкжмВтдТПМжБЭЈжаПМЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПОиаЮABCDжаЃЌAB=6ЃЌBC=8.ЕуPдкОиаЮABCDЕФФкВПЃЌЕуEдкБпBCЩЯЃЌТњзуЁїPBEЁзЁїDBCЃЌШєЁїAPDЪЧЕШбќШ§НЧаЮЃЌдђPEЕФГЄЮЊЪ§___________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌШчЭМЃЌОиаЮABCDЕФЖЅЕуAЃЌDЗжБ№дк![]() ЕФБпPMЃЌPNЩЯЃЌЖЅЕуBЁЂCдк
ЕФБпPMЃЌPNЩЯЃЌЖЅЕуBЁЂCдк![]() ЕФБпMNЩЯЧв
ЕФБпMNЩЯЧв![]() ЃЎ
ЃЎ
![]() ЧыдкЭМ1жадкЯпЖЮABЕФзѓВрЛвЛИіОиаЮEGBFЁзОиаЮABCDЃЌЪЙЕУЕуEЃЌЕуGЃЌЕуFЗжБ№дкЯпЖЮAMЁЂABЁЂMBЩЯ
ЧыдкЭМ1жадкЯпЖЮABЕФзѓВрЛвЛИіОиаЮEGBFЁзОиаЮABCDЃЌЪЙЕУЕуEЃЌЕуGЃЌЕуFЗжБ№дкЯпЖЮAMЁЂABЁЂMBЩЯ![]() БЃСєБивЊЕФКлМЃЃЌВЂзїМђЕЅЕФЫЕУї
БЃСєБивЊЕФКлМЃЃЌВЂзїМђЕЅЕФЫЕУї![]()
![]() ШєОиаЮABCDЕФБп
ШєОиаЮABCDЕФБп![]() ЃЌ
ЃЌ![]() ЃЌЧыМЦЫу
ЃЌЧыМЦЫу![]() жаОиаЮEGBFЕФБпГЄEFЕФГЄЖШЃЎ
жаОиаЮEGBFЕФБпГЄEFЕФГЄЖШЃЎ
![]() ШєОиаЮABCDЕФБп
ШєОиаЮABCDЕФБп![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() жаОиаЮEGBFЕФБпГЄEFЕФГЄЖШЮЊ______ЃЎ
жаОиаЮEGBFЕФБпГЄEFЕФГЄЖШЮЊ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDЕФБпГЄЮЊ4ЃЌЕуEЃЌFЗжБ№дкБпABЃЌADЩЯЃЌЧвЁЯECFЃН45ЁуЃЌCFЕФбгГЄЯпНЛBAЕФбгГЄЯпгкЕуGЃЌCEЕФбгГЄЯпНЛDAЕФбгГЄЯпгкЕуHЃЌСЌНгACЃЌEFЃЎЃЌGHЃЎ
ЃЈ1ЃЉЬюПеЃКЁЯAHCЁЁ ЁЁЁЯACGЃЛЃЈЬюЁАЃОЁБЛђЁАЃМЁБЛђЁАЃНЁБЃЉ
ЃЈ2ЃЉЯпЖЮACЃЌAGЃЌAHЪВУДЙиЯЕЃПЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЩшAEЃНmЃЌ
ЂйЁїAGHЕФУцЛ§SгаБфЛЏТ№ЃПШчЙћБфЛЏЃЎЧыЧѓГіSгыmЕФКЏЪ§ЙиЯЕЪНЃЛШчЙћВЛБфЛЏЃЌЧыЧѓГіЖЈжЕЃЎ
ЂкЧыжБНгаДГіЪЙЁїCGHЪЧЕШбќШ§НЧаЮЕФmжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACBЃН90ЁуЃЌCDЪЧABБпЩЯЕФжаЯпЃЌEЪЧCDЕФжаЕуЃЌЙ§ЕуCзїABЕФЦНааЯпНЛAEЕФбгГЄЯпгкЕуFЃЌСЌНгBFЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮBDCFЪЧСтаЮЃЛ
ЃЈ2ЃЉЕБRtЁїABCжаЕФБпЛђНЧТњзуЪВУДЬѕМўЪБЃПЫФБпаЮBDCFЪЧе§ЗНаЮЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈБОЬтТњЗж10ЗжЃЉЙХдЫКгЪЧбяжнЕФФИЧзКгЃЌЮЊДђдьЙХдЫКгЗчЙтДјЃЌЯжгавЛЖЮГЄЮЊ180УзЕФКгЕРећжЮШЮЮёгЩ![]() СНЙЄГЬЖгЯШКѓНгСІЭъГЩЃЎ
СНЙЄГЬЖгЯШКѓНгСІЭъГЩЃЎ![]() ЙЄзїЖгУПЬьећжЮ12УзЃЌ
ЙЄзїЖгУПЬьећжЮ12УзЃЌ![]() ЙЄГЬЖгУПЬьећжЮ8УзЃЌЙВгУЪБ20ЬьЃЎ
ЙЄГЬЖгУПЬьећжЮ8УзЃЌЙВгУЪБ20ЬьЃЎ
ЃЈ1ЃЉИљОнЬтвтЃЌМзЁЂввСНУћЭЌбЇЗжБ№СаГіЩаВЛЭъећЕФЗНГЬзщШчЯТЃК
![]()
![]()
![]()
![]() МзЃК
МзЃК ![]() ЁЁЁЁЁЁЁЁввЃК
ЁЁЁЁЁЁЁЁввЃК
ИљОнМзЁЂввСНУћЭЌбЇЫљСаЕФЗНГЬзщЃЌЧыФуЗжБ№жИГіЮДжЊЪ§![]() БэЪОЕФвтвхЃЌШЛКѓдкЗНПђжаВЙШЋМзЁЂввСНУћЭЌбЇЫљСаЕФЗНГЬзщЃК
БэЪОЕФвтвхЃЌШЛКѓдкЗНПђжаВЙШЋМзЁЂввСНУћЭЌбЇЫљСаЕФЗНГЬзщЃК
МзЃК![]() БэЪО________________ЃЌ
БэЪО________________ЃЌ![]() БэЪО_______________ЃЛ
БэЪО_______________ЃЛ
ввЃК![]() БэЪО________________ЃЌ
БэЪО________________ЃЌ![]() БэЪО_______________ЃЎ
БэЪО_______________ЃЎ
ЃЈ2ЃЉЧѓ![]() СНЙЄГЬЖгЗжБ№ећжЮКгЕРЖрЩйУзЃЎЃЈаДГіЭъећЕФНтД№Й§ГЬЃЉ
СНЙЄГЬЖгЗжБ№ећжЮКгЕРЖрЩйУзЃЎЃЈаДГіЭъећЕФНтД№Й§ГЬЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЩШаЮOABжаЃЌЁЯAOB=100ЁуЃЌOA=12ЃЌCЪЧOBЕФжаЕуЃЌCDЁЭOBНЛ![]() гкЕуDЃЌвдOCЮЊАыОЖЕФ
гкЕуDЃЌвдOCЮЊАыОЖЕФ![]() НЛOAгкЕуEЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЪЧЃЈЁЁЁЁЃЉ
НЛOAгкЕуEЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЪЧЃЈЁЁЁЁЃЉ

A. 12Іа+18![]() B. 12Іа+36
B. 12Іа+36![]() C. 6Іа+18
C. 6Іа+18![]() D. 6Іа+36
D. 6Іа+36![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
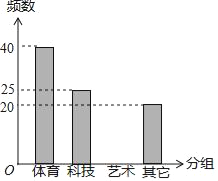
ЁОЬтФПЁПФГбЇаЃЮЊЕїВщбЇЩњЕФаЫШЄАЎКУЃЌГщВщСЫВПЗжбЇЩњЃЌВЂжЦзїСЫШчЯТБэИёгыЬѕаЮЭГМЦЭМЃК
ЦЕЪ§ | ЦЕТЪ | |
Ьхг§ | 40 | 0.4 |
ПЦММ | 25 | a |
веЪѕ | b | 0.15 |
ЦфЫќ | 20 | 0.2 |
ЧыИљОнЩЯЭМЭъГЩЯТУцЬтФПЃК
ЃЈ1ЃЉзмШЫЪ§ЮЊЁЁ ЁЁШЫЃЌa=ЁЁ ЁЁЃЌb=ЁЁ ЁЁЃЎ
ЃЈ2ЃЉЧыФуВЙШЋЬѕаЮЭГМЦЭМЃЎ
ЃЈ3ЃЉШєШЋаЃга600ШЫЃЌЧыФуЙРЫувЛЯТШЋаЃЯВЛЖвеЪѕРрбЇЩњЕФШЫЪ§гаЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯBACЃН90ЁуЃЌABЃН8cmЃЌACЃН6cmЃЌЖЏЕуPДгЕуCГіЗЂбиCBЗНЯђвд3cm/sЕФЫйЖШЯђЕуBдЫЖЏЃЌЭЌЪБЖЏЕуQДгЕуBГіЗЂбиBAЗНЯђвд2cm/sЕФЫйЖШЯђЕуAдЫЖЏЃЌНЋЁїAPQбижБЯпABЗелЕУЁїAPЁфQЃЌШєЫФБпаЮAPQPЁфЮЊСтаЮЃЌдђдЫЖЏЪБМфЮЊЃЈЁЁЁЁЃЉ
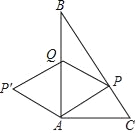
A. 1sB. ![]()
![]() sC.
sC. ![]() sD.
sD. ![]() s
s
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com