
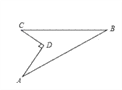
【题目】如图所示的一块地,已知AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m,求这块地的面积.
【答案】24m2
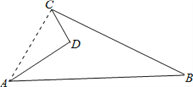
【解析】连接AC,利用勾股定理可以得出三角形ACD和ABC是直角三角形,△ABC的面积减去△ACD的面积就是所求的面积.
解:连接AC.
在Rt△ACD中,AD=4,CD=3,
∴AC 2 =AD 2 +CD 2 =4 2 +3 2 =25,
又∵AC>0,
∴AC=5.
又∵BC=12,AB=13,
∴AC 2 +BC 2 =5 2 +12 2 =169,
又∵AB 2 =169,
∴AC 2 +BC 2 =AB 2 ,
∴△ACB是直角三角形,
∴S =S △ABC -S △ADC =30-6=24m2.
“点睛”考查了直角三角形面积公式以及勾股定理的应用,作辅助线是解决本题的关键.


科目:初中数学 来源: 题型:
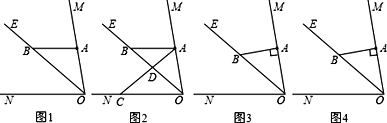
【题目】已知:∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D.设∠OAC=α.
(1)如图1,若AB∥ON,则:
①∠ABO的度数是 ;
②如图2,当∠BAD=∠ABD时,试求α的值(要说明理由);
(2)如图3,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,直接写出α的值;若不存在,说明理由.(自己画图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某化妆品专卖店,为了吸引顾客,在“母亲节”当天举办了甲、乙两种品牌化妆品有奖酬宾活动,凡购物满88元,均可得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机中一次连续摇出两个球,根据球的颜色决定送礼金券的多少(如下表):
甲种品牌 化妆品 | 球 | 两红 | 一红一白 | 两白 |
礼金卷(元) | 6 | 12 | 6 |
乙种品牌 化妆品 | 球 | 两红 | 一红一白 | 两白 |
礼金卷(元) | 12 | 6 | 12 |
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率;
(2)如果一个顾客当天在本店购物满88元,若只考虑获得最多的礼品卷,请你帮助分析选择购买哪种品牌的化妆品?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一、阅读理解:
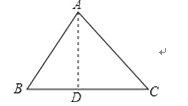
在△ABC中,BC=a,CA=b,AB=c;
(1)若∠C为直角,则a2+b2=c2;
(2)若∠C为锐角,则a2+b2与c2的关系为:a2+b2>c2;
(3)若∠C为钝角,试推导a2+b2与c2的关系.
二、探究问题:在△ABC中,BC=a=3,CA=b=4,AB=c,若△ABC是钝角三角形,求第三边c的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于平面内任一点P (a,b)若规定以下两种变换:①f(a,b)=(﹣a,﹣b),如f(1,2)=(﹣1,﹣2);②g(a,b)=(b,a),如g(1,3)=(3,1)按照以上变换,那么f(g(a,b))等于( )
A. (﹣b,﹣a) B. (a,b) C. (b,a) D. (﹣a,﹣b)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com