
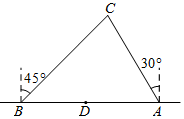
 如图,两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍船只停在C处海域,AB=60($\sqrt{3}$+1)海里,在B处测得C在北偏东45°反向上,A处测得C在北偏西30°方向上,在海岸线AB上有一灯塔D,测得AD=100海里.
如图,两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍船只停在C处海域,AB=60($\sqrt{3}$+1)海里,在B处测得C在北偏东45°反向上,A处测得C在北偏西30°方向上,在海岸线AB上有一灯塔D,测得AD=100海里.分析 (1)如图所示,过点C作CE⊥AB于点E,可求得∠CBD=45°,∠CAD=60°,设CE=x,在Rt△CBE与Rt△CAE中,分别表示出BE、AE的长度,然后根据AB=60($\sqrt{3}$+1)里,代入BE、AE的式子,求出x的值,继而可求出AC、BC的长度;
(2)如图所示,过点D作DF⊥AC于点F,在△ADF中,根据AD的值,利用三角函数的知识求出DF的长度,然后与100比较,进行判断.
解答 解: (1)如图所示,过点C作CE⊥AB于点E,
(1)如图所示,过点C作CE⊥AB于点E,
可得∠CBD=45°,∠CAD=60°,
设CE=x,
在Rt△CBE中,BE=CE=x,
在Rt△CAE中,AE=$\frac{\sqrt{3}}{3}$x,
∵AB=60($\sqrt{3}$+1)海里,
∴x+$\frac{\sqrt{3}}{3}$x=60($\sqrt{3}$+1),
解得:x=60$\sqrt{3}$,
则AC=$\frac{2\sqrt{3}}{3}$x=120,
BC=$\sqrt{2}$x=60$\sqrt{6}$,
答:A与C的距离为120海里,B与C的距离为60$\sqrt{6}$海里;
(2)如图所示,过点D作DF⊥AC于点F,
在△ADF中,
∵AD=100,∠CAD=60°,
∴DF=ADsin60°=50$\sqrt{3}$≈86.6<100,
故海监船沿AC前往C处盘查,有触礁的危险.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据题目中所给方向角构造直角三角形,然后利用三角函数的知识求解,难度适中.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
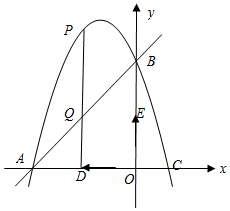 如图,抛物线经过点A(-3,0)、B(0,3),C(1,0).
如图,抛物线经过点A(-3,0)、B(0,3),C(1,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com