
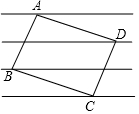
 如图,矩形ABCD的四个顶点正好落在四条平行线上,并且从上到下每两条平行线间的距离都是1,如果AB:BC=3:4,那么AB的长是$\frac{\sqrt{73}}{4}$.
如图,矩形ABCD的四个顶点正好落在四条平行线上,并且从上到下每两条平行线间的距离都是1,如果AB:BC=3:4,那么AB的长是$\frac{\sqrt{73}}{4}$. 分析 作辅助线,构建相似三角形,证明△ABE∽△BCF,列比例式求BE的长,利用勾股定理可以求AB的长.
解答 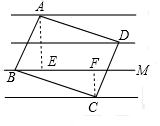 解:过A作AE⊥BM于E,过C作CF⊥BM于F,则CF=1,AE=2,
解:过A作AE⊥BM于E,过C作CF⊥BM于F,则CF=1,AE=2,
∴∠AEB=∠BFC=90°,
∴∠ABE+∠BAE=90°,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴∠ABE+∠CBE=90°,
∴∠BAE=∠CBE,
∴△ABE∽△BCF,
∴$\frac{AB}{BC}=\frac{BE}{CF}$,
∴$\frac{3}{4}=\frac{BE}{1}$,
∴BE=$\frac{3}{4}$,
在Rt△ABE中,AB=$\sqrt{{2}^{2}+(\frac{3}{4})^{2}}$=$\frac{\sqrt{73}}{4}$,
故答案为:$\frac{\sqrt{73}}{4}$.
点评 本题考查了矩形的性质、相似三角形的判定与性质、两平行线的距离以及勾股定理;熟练掌握矩形的性质,证明三角形相似是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
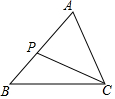 如图,已知在△ABC中,P为AB上一点,连接CP,以下条件中不能判定△ACP∽△ABC的是( )
如图,已知在△ABC中,P为AB上一点,连接CP,以下条件中不能判定△ACP∽△ABC的是( )| A. | ∠ACP=∠B | B. | ∠APC=∠ACB | C. | $\frac{AC}{AB}=\frac{CP}{BC}$ | D. | $\frac{AC}{AP}=\frac{AB}{AC}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  清华大学 | B. |  浙江大学 | C. |  北京大学 | D. |  中南大学 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
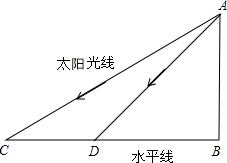 在同一时刻太阳光线与水平线的夹角是一定的.如图,有一垂直于地面的物体AB.在某一时刻太阳光线与水平线的夹角为30°时,物体AB的影长BC为4米;在另一个时刻太阳光线与水平线的夹角为45°时,则物体AB的影长BD为$\frac{4\sqrt{3}}{3}$米.(结果保留根号)
在同一时刻太阳光线与水平线的夹角是一定的.如图,有一垂直于地面的物体AB.在某一时刻太阳光线与水平线的夹角为30°时,物体AB的影长BC为4米;在另一个时刻太阳光线与水平线的夹角为45°时,则物体AB的影长BD为$\frac{4\sqrt{3}}{3}$米.(结果保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com