
 请根据下列图表信息解答问题:
请根据下列图表信息解答问题:| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 年增长率 | 31% | 27% | 32% | 35% | 52% |
分析 (1)根据折线统计图可以得到2016年的年增长率;
(2)根据平均数与中位数的定义求解;
(3)根据条象形统计图和扇形统计图可以解答本题.
解答 解:(1)由题意可得,
2016年的年增长率是:(13.72-12.60)÷12.60×100%≈9%,
故答案为:9%;
(2)统计表中增长率的平均数为:(31%+27%+32%+35%+52%+9%)÷6=31%;
将它们按从小到大的顺序排列为:9%,27%,31%,32%,35%,52%,
所以中位数是(31%+32%)÷2=31.5%;
(3)2017年的观影人次为:13.72×(1+31%)≈17.97(人次),
预估的理由是:由折线统计图和表格可知,最近6年增长率的平均数为31%,故预估2016年的增长率为31%.
点评 本题考查条形统计图、中位数与平均数,解题的关键是明确题意,找出所求问题需要的条件.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:解答题
 如图,平行四边形ABCD中,AC与BD相交于点O,AB=AC,延长BC到点E,使CE=BC,连接AE,分别交BD、CD于点F、G.
如图,平行四边形ABCD中,AC与BD相交于点O,AB=AC,延长BC到点E,使CE=BC,连接AE,分别交BD、CD于点F、G.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
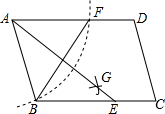 如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=4,则AE的长为( )
如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=4,则AE的长为( )| A. | $\sqrt{7}$ | B. | 2$\sqrt{7}$ | C. | 3$\sqrt{7}$ | D. | 4$\sqrt{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com