
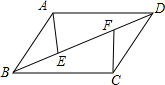
 如图所示,已知点E,F在?ABCD的对角线BD上,且BF=DE,求证:AE=CF.
如图所示,已知点E,F在?ABCD的对角线BD上,且BF=DE,求证:AE=CF. 分析 根据平行四边形的性质可得AD∥BC,AD=BC,根据平行线的性质可得∠EDA=∠FBC,再加上条件ED=BF可利用SAS判定△AED≌△CFB,进而可得AE=CF.
解答 证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠EDA=∠FBC,
在△AED和△CFB中,$\left\{\begin{array}{l}{AD=BC}&{\;}\\{∠ADE=∠CBF}&{\;}\\{BF=DE}&{\;}\end{array}\right.$,
∴△AED≌△CFB(SAS),
∴AE=CF.
点评 此题主要考查了平行四边形的性质和全等三角形的判定和性质,关键是掌握平行四边形对边平行且相等.


科目:初中数学 来源: 题型:选择题
| A. | 5.63×104 | B. | 5.63×105 | C. | 56.3×104 | D. | 0.563×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
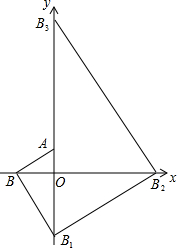 把多块大小不同的30°直角三角板如图所示,摆放在平面直角坐标系中,第一块三角板AOB的一条直角边与y轴重合且点A的坐标为(0,1),∠ABO=30°;第二块三角板的斜边BB1与第一块三角板的斜边AB垂直且交y轴于点B1;第三块三角板的斜边B1B2与第二块三角板的斜边BB1垂直且交x轴于点B2;第四块三角板的斜边B2B3与第三块三角板的斜边B1B2垂直且交y轴于点B3;…按此规律继续下去,则点B2017的坐标为(0,-31009).
把多块大小不同的30°直角三角板如图所示,摆放在平面直角坐标系中,第一块三角板AOB的一条直角边与y轴重合且点A的坐标为(0,1),∠ABO=30°;第二块三角板的斜边BB1与第一块三角板的斜边AB垂直且交y轴于点B1;第三块三角板的斜边B1B2与第二块三角板的斜边BB1垂直且交x轴于点B2;第四块三角板的斜边B2B3与第三块三角板的斜边B1B2垂直且交y轴于点B3;…按此规律继续下去,则点B2017的坐标为(0,-31009).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{x}{5}}$ | B. | $\sqrt{8}$ | C. | $\sqrt{3{x}^{2}y}$ | D. | $\sqrt{{x}^{2}-9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解我市上班族的收入情况 | |
| B. | 了解全市市民的身高情况 | |
| C. | 了解某班学生期末考数学科成绩情况 | |
| D. | 了解我市的空气污染情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 某校七年级某班期末测试全班所有学生数学成绩的频数分布直方图如图所示(满分100分),则该班成绩在85.5~95.5这一分数段的学生数是30.
某校七年级某班期末测试全班所有学生数学成绩的频数分布直方图如图所示(满分100分),则该班成绩在85.5~95.5这一分数段的学生数是30.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
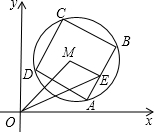 如图,已知M(3,3),⊙M的半径为2,四边形ABCD是⊙M的内接正方形,E为AB中点,当正方形ABCD绕圆心M转动时,△OME的面积最大值为3.
如图,已知M(3,3),⊙M的半径为2,四边形ABCD是⊙M的内接正方形,E为AB中点,当正方形ABCD绕圆心M转动时,△OME的面积最大值为3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com