
【题目】如图,一张正方形纸板的边长为2cm,将它剪去4个全等的直角三角形(图中阴影部分).设AE=BF=CG=DH=xcm,四边形EFGH的面积为ycm2 , 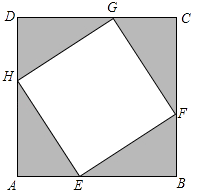
(1)求y关于x的函数表达式和自变量x的取值范围;
(2)求四边形EFGH的面积为3cm2时的x值;
(3)四边形EFGH的面积可以为1.5cm2吗?请说明理由.
【答案】
(1)解:∵在正方形纸上剪去4个全等的直角三角形,
∴∠AHE=∠DGH,∠DGH+∠DHG=90°,HG=HE,
∵∠EHG=180°﹣∠AHE﹣∠DHG,
∴∠EHG=90°,四边形EFGH为正方形,
在△AEH中,AE=x,AH=BE=AB﹣AE=2﹣x,∠A=90°,
∴HE2=AE2+AH2=x2+(2﹣x)2=2x2﹣4x+4,
正方形EFGH的面积y=HE2=2x2﹣4x+4,
∵AE,AH均为正值,
∴0<x<2,
故y关于x的函数表达式为:y=2x2﹣4x+4,自变量x的取值范围0<x<2.
(2)解:将y=3代入y=2x2﹣4x+4中,整理得:2x2﹣4x+1=0,
解得:x1=1+ ![]() ,x2=1﹣
,x2=1﹣ ![]() ,
,
故四边形EFGH的面积为3cm2时的x的值为1+ ![]() 或1﹣
或1﹣ ![]() .
.
(3)解:四边形EFGH的面积为:y=2x2﹣4x+4=2(x﹣1)2+2,(0<x<2),
∵(x﹣1)2≥0,
∴y≥2,
四边形EFGH的面积不能为1.5cm2.
【解析】(1)先证出四边形EFGH为正方形,用未知数x表示其任一边长,根据正方形面积公式即可解决问题;(2)代入y值,解一元二次方程即可;(3)将面积y=2x2﹣4x+4改写成完全平方的形式,可得知y≥2,故不能为cm2 .


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案科目:初中数学 来源: 题型:
【题目】设边长为3的正方形的对角线长为a.下列关于a的四种说法: ①a是无理数;
②a可以用数轴上的一个点来表示;
③3<a<4;
④a是18的算术平方根.
其中,所有正确说法的序号是( )
A.①④
B.②③
C.①②④
D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,BC=AC,以BC为直径的⊙O与边AB、AC分别交于点D,E,DF⊥AC于点F. 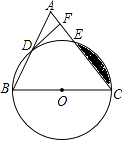
(1)求证:点D是AB的中点;
(2)判断DF与⊙O的位置关系,并证明你的结论;
(3)若⊙O的直径为20,cosB= ![]() ,求阴影部分面积.
,求阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,抛物线y=ax2﹣ax+6与x轴负半轴交于点A,与x轴的正半轴交于点B,且AB=7.
(1)如图1,求a的值;
(2)如图2,点P在第一象限内抛物线上,过P作PH∥AB,交y轴于点H,连接AP,交OH于点F,设HF=d,点P的横坐标为t,求d与t之间的函数关系式,并直接写出t的取值范围;
(3)如图3,在(2)的条件下,当PH=2d时,将射线AP沿着x轴翻折交抛物线于点M,在抛物线上是否存在点N,使∠AMN=45°,若存在,求出点N的坐标.若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年《政府工作报告》中提出了十大新词汇,为了解同学们对新词汇的关注度,某数学兴趣小组选取其中的A:“互联网+政务服务”,B:“工匠精神”,C:“光网城市”,D:“大众旅游时代”四个热词在全校学生中进行了抽样调查,要求被调查的每位同学只能从中选择一个我最关注的热词.根据调查结果,该小组绘制了如下的两幅不完整的统计图. 
请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了多少名同学?
(2)条形统计图中,m= , n=;
(3)扇形统计图中,热词B所在扇形的圆心角是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点D、E分别在△ABC的边AB、AC上,下列给出的条件中,不能判定DE∥BC的是( )
A.BD:AB=CE:AC
B.DE:BC=AB:AD
C.AB:AC=AD:AE
D.AD:DB=AE:EC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com