
在平面直角坐标系中 ,已知抛物线
,已知抛物线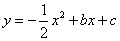 (
(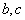 为常数)的顶点为
为常数)的顶点为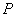 ,等腰直角三角形
,等腰直角三角形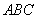 的定点
的定点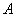 的坐标为
的坐标为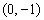 ,
,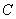 的坐标为
的坐标为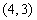 ,直角顶点
,直角顶点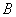 在第四象限.
在第四象限.
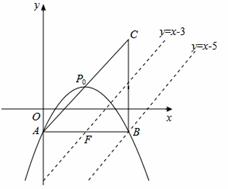
(1)如图,若该抛物线过 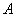 ,
,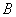 两点,求该抛物线的函数表达式;(3分)
两点,求该抛物线的函数表达式;(3分)
(2)平移(1)中的抛物线,使顶点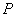 在直线
在直线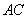 上滑动,且与
上滑动,且与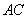 交于另一点
交于另一点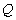 .
.
i)若点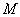 在直线
在直线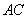 下方,且为平移前(1)中抛物线上的点,当以
下方,且为平移前(1)中抛物线上的点,当以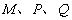
三点为顶点的三角形是等腰直角三角形时,求所有符合条件的点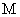 的坐标;(4分)
的坐标;(4分)
ii)取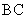 的中点
的中点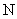 ,连接
,连接 .试探究
.试探究 是否存在最大值?若存在,求出该最大值;若不存在,请说明理由. (2分)
是否存在最大值?若存在,求出该最大值;若不存在,请说明理由. (2分)
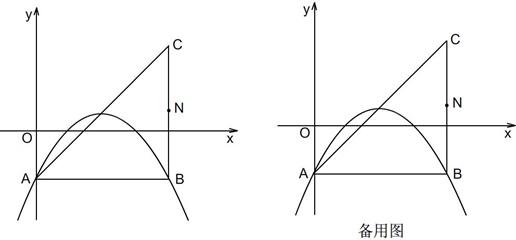
解(1)A(0,-1) C(4,3)
则|AC|=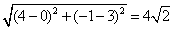
ABC为等腰直角三角形 ∴AB=BC=4
∴B点(4,-1)将A,B代入抛物线方程有
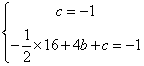 ⇒
⇒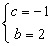
∴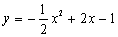 …………………………………..3
…………………………………..3
(2)当顶点P在直线AC上滑动时,平移后抛物线与AC另一交点Q就是A点沿直线AC滑动同样的单位。
原抛物线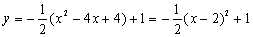
∴顶点P为(2,1)
设平移后顶点P为(a,a-1),
则平移后抛物线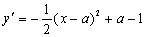
联立y=x-1(直线AC方程) 得Q点为(a-2,a-3)∴|PQ|=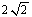
即实际上是线段AP在直线AC上的滑动.
ⅰ)点M在直线AC下方,且M,P,Q构成等腰直角三角形,
那么先考虑使MP,Q构成等腰直角三角形的M点的轨迹,
再求其轨迹与抛物线的交点以确定M点.
① 若∠M为直角,
则M点轨迹即为AC下方距AC为MH且与AC平行的直线l
又知|PQ|=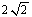 ,则|MH|=
,则|MH|=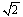 |PM|=2
|PM|=2
直线l即为AC向下平移|PM|=2个单位 L:y=x-3 联立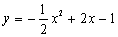
得x=1±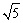 M点为(1+
M点为(1+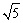 ,
,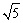 -2)或(1-
-2)或(1-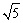 ,-
,-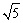 -2)…………………………5
-2)…………………………5
② 若∠P=或∠Q为直角,即PQ为直角边,MQ⊥PQ且,MQ=PQ=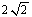
或MP⊥PQ,且MP=PQ=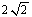 ,∴M点轨迹是AC下方距AC为
,∴M点轨迹是AC下方距AC为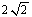 且与AC平行直线L
且与AC平行直线L
直线L即为AC向下平移|MP|=4个单位L:y=x-5联立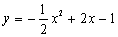
 得x=4或x=-2∴M点为(4,-1)或(-2,-7)
得x=4或x=-2∴M点为(4,-1)或(-2,-7)
综上所有符合条件的点M为(1+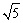 ,
,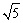 -2)(4,-1);
-2)(4,-1);
(1-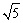 ,-
,-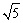 -2),(-2,-7)…………………7
-2),(-2,-7)…………………7
ⅱ)(特别说明:解答中的M都应该换成F)
知PQ=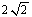
 有最大值,即NP+BQ有最小值
有最大值,即NP+BQ有最小值
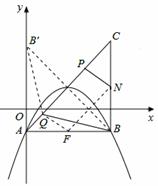
如下图,取AB中点F,连结QF,NF,知N为中点∴FN为AC边中位线,∴FN∥AC且FN=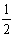 AC=
AC=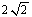 =PQ∴
=PQ∴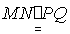 ∴FNPQ为平行四边形
∴FNPQ为平行四边形
即PN=QF ∴QB+PN=BQ+FQ 此时,作B点关于AC对称的点B′,连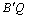 ,
,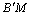
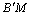 交AC于点H,易知
交AC于点H,易知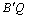 =BQ
=BQ
∴BQ+PN=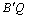 +FQ≥
+FQ≥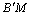 (三角形两边之和大于第三边)仅当Q与H重合时,取等号
(三角形两边之和大于第三边)仅当Q与H重合时,取等号
即BQ+PN最小值存在 且最小值为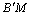 连结
连结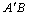 知
知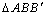 为等腰直角三角形。
为等腰直角三角形。
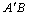 =4,AF=
=4,AF=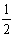 AB=2 ∴由勾股定理得
AB=2 ∴由勾股定理得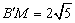
∴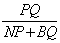 最大值存在,且最大值为
最大值存在,且最大值为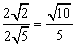 ………………9
………………9
 |


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
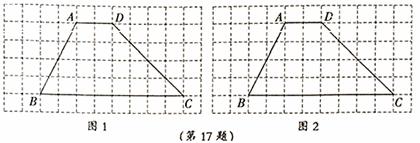
已知梯形ABCD,请使用无刻度直尺画图。
(1)在图1中画一个与梯形ABCD面积相等,且以CD为边的三角形;
(2)在图2中画一个与梯形ABCD面积相等,且以AB为边的平行四边形。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,路灯OP距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B处时,人影的长度( )
A、变长了1.5米 B、变短了2.5米 C、变长了3.5米 D、变短了3.5米 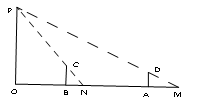
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,等腰直角 △ABC 中, AC=BC,∠ACB =900, AF 为△ABC的角平分线,分别过点 C, B 作 AF 的垂线,垂足分别为 E ,D.以下结论:① CE=DE=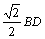 ;② AF= 2BD ;③ CE+ EF=
;② AF= 2BD ;③ CE+ EF=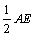 ;④
;④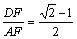 .其中结论正确的序号是( )
.其中结论正确的序号是( )
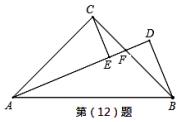
(A)①②③ (B)①②④ (C)①③④ (D)②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
据 2016 年 2 月 14 日《每日新报》报道,春节七天假期,天津市共接待游客约4 412 600 人次.将 4 412 600 用科学记数法表示应为( )
(A)0.44126×107 (B)4.4126×106 (C)44.126×105 (D)44126×102
查看答案和解析>>
科目:初中数学 来源: 题型:
(1)已知∠α和线段m,h,用直尺和圆规作▱ABCD,使AB=m,∠DAB=∠α,AB和CD之间的距离为h(作出图形,不写作法,保留痕迹)
(2)在(1)中,若m比h大2,且m与h的和小于10,求h的取值范围.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com