练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    运用平行四边形的性质解决以下计算问题：

    (1)如图，若ABCD的周长为22厘米，AC，BD相交于O，△DOA的周长比△AOB的周长小3厘米，则AD，AB的长分别为多少？

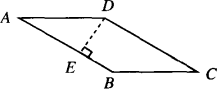
    (2)如图，在ABCD中，∠A＝30°，AB＝20厘米，AD＝15厘米，则ABCD的周长和面积分别为多少？

    答案：
    解析：

    　　解：(1)由题意知，BO＝DO，故由△DOA的周长比△AOB的周长小3厘米，即有AB－AD＝3厘米，又由平行四边形ABCD的周长为22厘米，可知AB＋AD＝11厘米，解方程组得AD＝4厘米，AB＝7厘米．

    　　(2)由已知得ABCD的周长易求，应为2×(20＋15)＝70厘米；过D点作DE⊥AB于E，由∠A＝30°知DE＝AD/2＝7.5厘米，故ABCD的面积为AB·DE＝20×7.5＝150厘米2．

    　　评析：(1)题为教材中95页第1题和100页第3题的变式题，此类问题重在考查对平行四边形对边相等及对角线互相平分的性质的灵活应用．(2)题为教材中94页例2及101页12题的变式问题，重在考查平行四边形面积的计算，要灵活地“作高求高”，同时还要综合运用到特殊角带来的特殊性质或勾股定理等．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    数学学习总是如数学知识自身的生长历史一样，往往起源于猜测中的发现，我们所发现的不一定对，但是当利用我们已有的知识作为推理的前提论证之后，当所发现的在逻辑上没有矛盾之后，就可以作为新的推理的前提，数学中称之为定理．
    （1）尝试证明：
    等腰三角形的探索中借助折纸发现：直角三角形斜边上的中线等于斜边的一半．但是当时并未说明这个结论的合理．现在我们学些了矩形的判定和性质之后，就可以解决这个问题了．如图1若在Rt△ABC中CD是斜边AB的中线，则CD=
    12
    AB    ，你能用矩形的性质说明这个结论吗？请说明．
    （2）迁移运用：利用上述结论解决下列问题：
    ①如图2所示，四边形ABCD中，∠BAD=90°，∠DCB=90°，EF分别是BD、AC的中点，请你说明EF与AC的位置关系．
    ②如图3所示，?ABCD中，以AC为斜边作Rt△ACE，∠AEC=90°，且∠BED=90°，试说明平行四边形ABCD是矩形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    数学学习总是如数学知识自身的生长历史一样，往往起源于猜测中的发现，我们所发现的不一定对，但是当利用我们已有的知识作为推理的前提论证之后，当所发现的在逻辑上没有矛盾之后，就可以作为新的推理的前提，数学中称之为定理．
    （1）尝试证明：
    等腰三角形的探索中借助折纸发现：直角三角形斜边上的中线等于斜边的一半．但是当时并未说明这个结论的合理．现在我们学些了矩形的判定和性质之后，就可以解决这个问题了．如图1若在Rt△ABC中CD是斜边AB的中线，则数学公式，你能用矩形的性质说明这个结论吗？请说明．
    （2）迁移运用：利用上述结论解决下列问题：
    ①如图2所示，四边形ABCD中，∠BAD=90°，∠DCB=90°，EF分别是BD、AC的中点，请你说明EF与AC的位置关系．
    ②如图3所示，?ABCD中，以AC为斜边作Rt△ACE，∠AEC=90°，且∠BED=90°，试说明平行四边形ABCD是矩形．

    查看答案和解析>>

    同步练习册答案