
分析 分子、分母同时乘以($\sqrt{5}$-$\sqrt{3}$)即可.
解答 解:$\frac{2}{\sqrt{5}+\sqrt{3}}$=$\frac{2(\sqrt{5}-\sqrt{3})}{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}$=$\frac{2(\sqrt{5}-\sqrt{3})}{(\sqrt{5})^{2}-({\sqrt{3})}^{2}}$=$\sqrt{5}$-$\sqrt{3}$.
故答案是:$\sqrt{5}$-$\sqrt{3}$.
点评 主要考查二次根式的有理化.根据二次根式的乘除法法则进行二次根式有理化.二次根式有理化主要利用了平方差公式,所以一般二次根式的有理化因式是符合平方差公式的特点的式子.即一项符号和绝对值相同,另一项符号相反绝对值相同.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
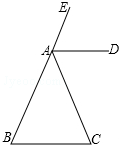 如图,已知在△ABC中,有三个事项①AD平分∠EAC ②AD∥BC,③∠B=∠C,请你选择其中的两个事项作为条件,另一个事项作为结论,例如:已知①AD平分∠EAC,②AD∥BC,求证③∠B=∠C.你的选择是:已知②AD∥BC,③∠B=∠C,求证①AD平分∠EAC 请说明理由.
如图,已知在△ABC中,有三个事项①AD平分∠EAC ②AD∥BC,③∠B=∠C,请你选择其中的两个事项作为条件,另一个事项作为结论,例如:已知①AD平分∠EAC,②AD∥BC,求证③∠B=∠C.你的选择是:已知②AD∥BC,③∠B=∠C,求证①AD平分∠EAC 请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com