
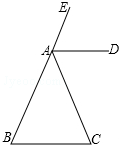
 如图,已知在△ABC中,有三个事项①AD平分∠EAC ②AD∥BC,③∠B=∠C,请你选择其中的两个事项作为条件,另一个事项作为结论,例如:已知①AD平分∠EAC,②AD∥BC,求证③∠B=∠C.你的选择是:已知②AD∥BC,③∠B=∠C,求证①AD平分∠EAC 请说明理由.
如图,已知在△ABC中,有三个事项①AD平分∠EAC ②AD∥BC,③∠B=∠C,请你选择其中的两个事项作为条件,另一个事项作为结论,例如:已知①AD平分∠EAC,②AD∥BC,求证③∠B=∠C.你的选择是:已知②AD∥BC,③∠B=∠C,求证①AD平分∠EAC 请说明理由.  数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
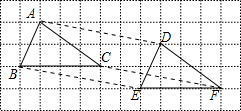 经过平移,△ABC移到△DEF的位置,如图,下列结论:①AD=BE=CF,且AD∥BE∥CF;②AB∥DE,BC∥EF,BC=EF;③AB=DE,BC=EF,AC=DF.正确的有( )
经过平移,△ABC移到△DEF的位置,如图,下列结论:①AD=BE=CF,且AD∥BE∥CF;②AB∥DE,BC∥EF,BC=EF;③AB=DE,BC=EF,AC=DF.正确的有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
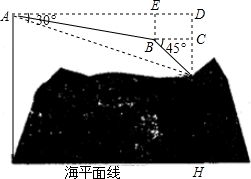 2015年4月25日,尼泊尔发生强烈地震,中国西藏部分地区也被波及,我国空军派出直升飞机“直九”抢险救灾,在一次执行运送药品及食品的任务时,“直九”军机飞行高度已知稳定在3500米,到达航线A出时测得樟木边防站M的俯角为26.5°,保持航向不变前行1700米到达E处,再匀速垂直下降500米到达B处后,测得边防站M的俯角为45°,计算:
2015年4月25日,尼泊尔发生强烈地震,中国西藏部分地区也被波及,我国空军派出直升飞机“直九”抢险救灾,在一次执行运送药品及食品的任务时,“直九”军机飞行高度已知稳定在3500米,到达航线A出时测得樟木边防站M的俯角为26.5°,保持航向不变前行1700米到达E处,再匀速垂直下降500米到达B处后,测得边防站M的俯角为45°,计算:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
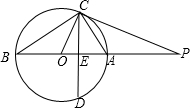 如图,AB是⊙O的直径,点P在BA的延长线上,点A是$\widehat{CD}$的中点,∠POC=∠PCE.
如图,AB是⊙O的直径,点P在BA的延长线上,点A是$\widehat{CD}$的中点,∠POC=∠PCE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com