
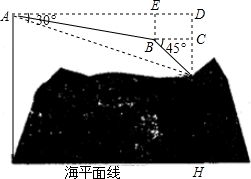
 2015年4月25日,尼泊尔发生强烈地震,中国西藏部分地区也被波及,我国空军派出直升飞机“直九”抢险救灾,在一次执行运送药品及食品的任务时,“直九”军机飞行高度已知稳定在3500米,到达航线A出时测得樟木边防站M的俯角为26.5°,保持航向不变前行1700米到达E处,再匀速垂直下降500米到达B处后,测得边防站M的俯角为45°,计算:
2015年4月25日,尼泊尔发生强烈地震,中国西藏部分地区也被波及,我国空军派出直升飞机“直九”抢险救灾,在一次执行运送药品及食品的任务时,“直九”军机飞行高度已知稳定在3500米,到达航线A出时测得樟木边防站M的俯角为26.5°,保持航向不变前行1700米到达E处,再匀速垂直下降500米到达B处后,测得边防站M的俯角为45°,计算:分析 (1)在Rt△AEB中,根据勾股定理即可求得AB的长;
(2)设DM=x,则MC=x-500,在等腰直角△BCM中,BC=CM=x-500,即可求得AD=1200+x,然后在△ADM中利用三角函数的定义列出关于x的方程,解方程即可求解.
解答 解:(1)在RT△AEB中,AB=$\sqrt{A{E}^{2}+E{B}^{2}}$=$\sqrt{170{0}^{2}+50{0}^{2}}$≈1772(米);
(2)设DM=x,则MC=DM-DC=DM-EB=x-500,
在RT△BCM中,BC=$\frac{MC}{tan45°}$=x-500,
故ED=BC=x-500,AD=AE+ED=1700+x-500=1200+x,
在RT△ADM中,tan∠DAM=$\frac{DM}{AD}$,tan26.5°=$\frac{x}{1200+x}$,
即$\frac{1}{2}$=$\frac{x}{1200+x}$,解得x=1200,
经检验,x=1200是方程的解,
此时MH=3500-1200=2300,
所以樟木边防站的海拔高度为2300米.
点评 本题考查了解直角三角形的应用-仰角俯角问题,难度适中,通过构造直角三角形,利用三角函数求解是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
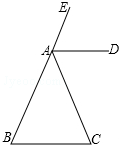 如图,已知在△ABC中,有三个事项①AD平分∠EAC ②AD∥BC,③∠B=∠C,请你选择其中的两个事项作为条件,另一个事项作为结论,例如:已知①AD平分∠EAC,②AD∥BC,求证③∠B=∠C.你的选择是:已知②AD∥BC,③∠B=∠C,求证①AD平分∠EAC 请说明理由.
如图,已知在△ABC中,有三个事项①AD平分∠EAC ②AD∥BC,③∠B=∠C,请你选择其中的两个事项作为条件,另一个事项作为结论,例如:已知①AD平分∠EAC,②AD∥BC,求证③∠B=∠C.你的选择是:已知②AD∥BC,③∠B=∠C,求证①AD平分∠EAC 请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.1×108 | B. | 110×108 | C. | 1.1×1010 | D. | 0.11×1011 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com